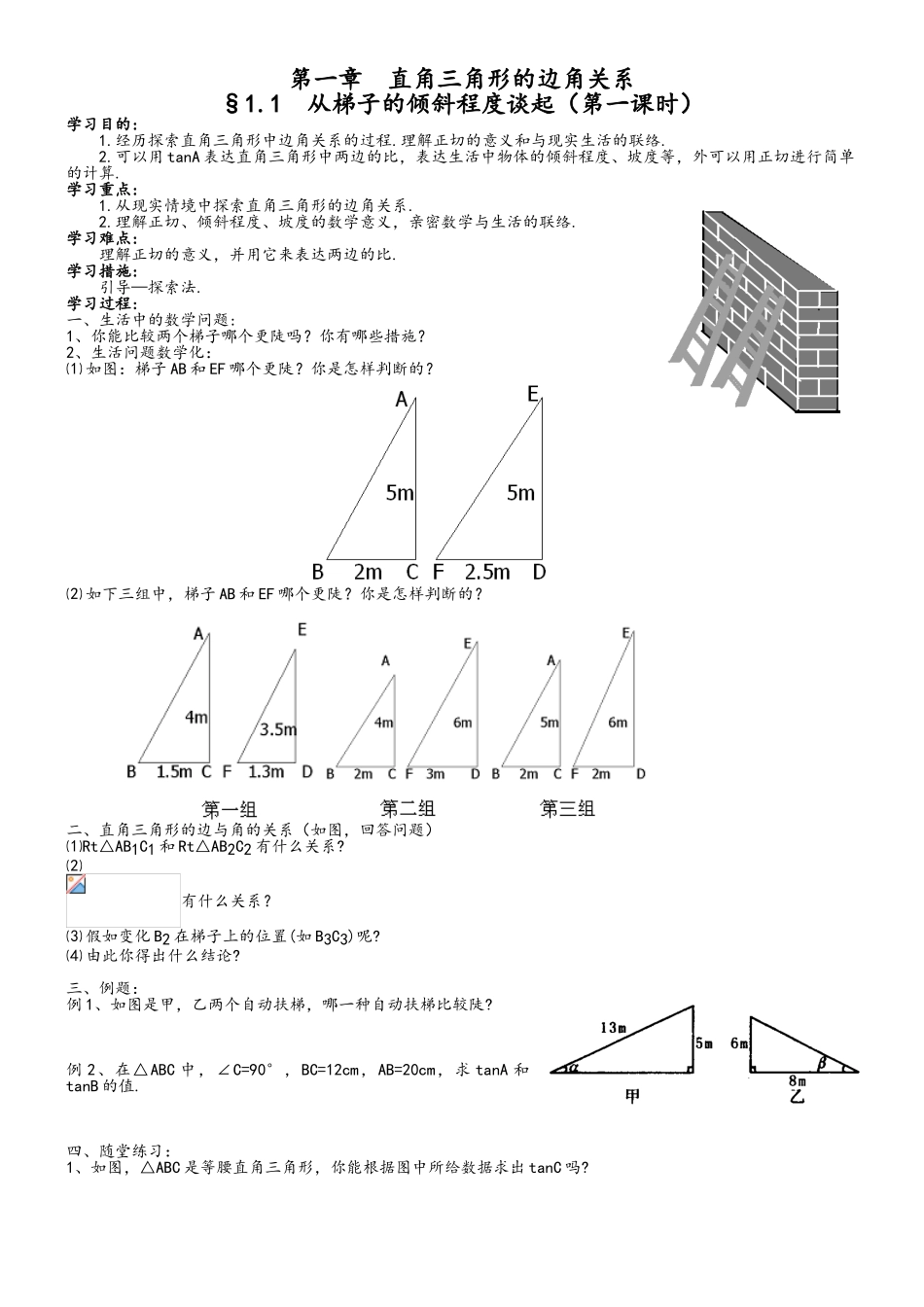
第一章 直角三角形的边角关系§1.1 从梯子的倾斜程度谈起(第一课时)学习目的:1.经历探索直角三角形中边角关系的过程.理解正切的意义和与现实生活的联络.2.可以用 tanA 表达直角三角形中两边的比,表达生活中物体的倾斜程度、坡度等,外可以用正切进行简单的计算.学习重点:1.从现实情境中探索直角三角形的边角关系.2.理解正切、倾斜程度、坡度的数学意义,亲密数学与生活的联络.学习难点:理解正切的意义,并用它来表达两边的比.学习措施:引导—探索法.学习过程:一、生活中的数学问题:1、你能比较两个梯子哪个更陡吗?你有哪些措施?2、生活问题数学化:⑴ 如图:梯子 AB 和 EF 哪个更陡?你是怎样判断的?⑵ 如下三组中,梯子 AB 和 EF 哪个更陡?你是怎样判断的?二、直角三角形的边与角的关系(如图,回答问题)⑴Rt△AB1C1 和 Rt△AB2C2 有什么关系?⑵有什么关系?⑶ 假如变化 B2 在梯子上的位置(如 B3C3)呢?⑷ 由此你得出什么结论?三、例题:例 1、如图是甲,乙两个自动扶梯,哪一种自动扶梯比较陡?例 2、在△ABC 中,∠C=90°,BC=12cm,AB=20cm,求 tanA 和tanB 的值.四、随堂练习:1、如图,△ABC 是等腰直角三角形,你能根据图中所给数据求出 tanC 吗?2、如图,某人从山脚下的点 A 走了 200m 后抵达山顶的点 B,已知点 B 到山脚的垂直距离为 55m,求山的坡度.(成果精确到 0.001)3、若某人沿坡度 i=3:4 的斜坡前进 10 米,则他所在的位置比本来的位置升高________米.4、菱形的两条对角线分别是 16 和 12.较长的一条对角线与菱形的一边的夹角为 θ,则 tanθ=______.5、如图,Rt△ABC 是一防洪堤背水坡的横截面图,斜坡 AB 的长为 12 m,它的坡角为45°,为了提高该堤的防洪能力,现将背水坡改导致坡比为 1:1.5 的斜坡 AD,求 DB的长.(成果保留根号) 五、课后练习:1、在 Rt△ABC 中,∠C=90°,AB=3,BC=1,则 tanA= _______.2、在△ABC 中,AB=10,AC=8,BC=6,则 tanA=_______.3、在△ABC 中,AB=AC=3,BC=4,则 tanC=______.4、在 Rt△ABC 中,∠C 是直角,∠A、∠B、∠C 的对边分别是 a、b、c,且 a=24,c= 25,求 tanA、tanB 的值.5、若三角形三边的比是 25:24:7,求最小角的正切值.6、如图,在菱形 ABCD 中,AE⊥BC 于 E,EC=1,tanB=, 求菱形的边长和四边形 AECD 的周长.7、已知:如图,斜坡 AB 的倾斜角 a,且 tanα=,既有一小球从坡底 A 处以 20cm/s 的...