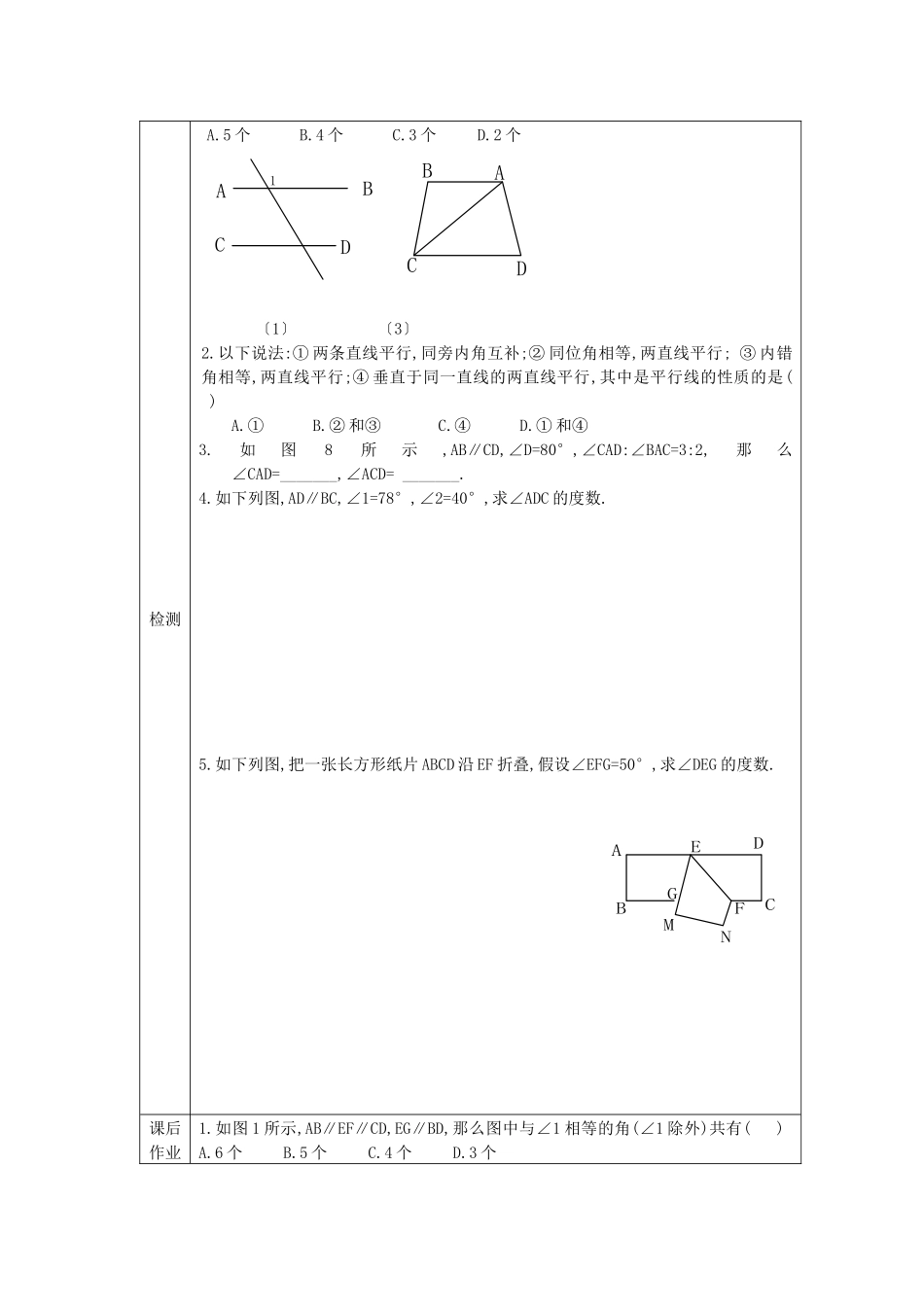
第 1 课时 平行线的性质学习目标1.知道平行线的性质。2.会用平行线的性质重点平行线的性质难点平行线的性质的应用导学过程师生活动一、情境导入我们知道,同位角相等,内错角相等,或同旁内角互补,可以判定两直线平行。反过来,假如两条直线平行,那么同位角、内错角、同旁内角有怎样的数量关系呢 二、导学〔一〕探究性质一1.学生画图:用直尺和三角尺画出两条平行线 a∥b,再画一条直线 c 与直线 a,b相交,如以下列图。2.测量这些角的度数,把结果填入表内:角∠1∠2∠3∠4度数3.根据测量所得数据作出猜想:图中哪些角是同位角它们具有怎样的数量关系在详尽分析后,写出猜想。 4.学生验证猜想:再任意画一条直线 d 与直线 a,b 相交,度量并计算各同位角的度数,你的猜想还成立吗4.归纳平行线的性质 1:两条平行线被第三条直线所截, 相等。简称 , 几何语言: 〔二〕探究性质二、三1.学生自学教材 19 页思考——例 1 之前2.归纳性质 2: 直线 a、b 被直线 c 所截,且 a b,∥求证:1=2.∠∠证明:两条平行线被第三条直线所截, 相等。简称 , 几何语言: 2.归纳性质 3: 直线 a、b 被直线 c 所截,且 a b,∥求证:1+2=180º.∠∠证明:两条平行线被第三条直线所截, 相等。简称 , 几何语言: 三、精讲点拔例 1.如图〔1〕,直线,,那么∠2、∠3、∠4 各是多少度稳固练习:如图,要设计一个弯形管道,求管道,那么如何设计的角度呢稳固提高:如图〔3〕,是一条直线,,求的度数四、学习小结这节课的收获:学后反思达标1.如图 1 所示,AB∥CD,那么与∠1 相等的角(∠1 除外)共有( )检测A.5 个 B.4 个 C.3 个 D.2 个 〔1〕 〔3〕2.以下说法:① 两条直线平行,同旁内角互补;② 同位角相等,两直线平行;③ 内错角相等,两直线平行;④ 垂直于同一直线的两直线平行,其中是平行线的性质的是( ) A.① B.② 和③ C.④ D.① 和④3.如图8所示,AB∥CD,∠D=80°,∠CAD:∠BAC=3:2,那么∠CAD=_______,∠ACD=_______.4.如下列图,AD∥BC,∠1=78°,∠2=40°,求∠ADC 的度数.5.如下列图,把一张长方形纸片 ABCD 沿 EF 折叠,假设∠EFG=50°,求∠DEG 的度数.课后作业1.如图 1 所示,AB∥EF∥CD,EG∥BD,那么图中与∠1 相等的角(∠1 除外)共有( ) A.6 个 B.5 个 C.4 个 D.3 个DCBA1DCBANMGFEDCBA 〔1〕 〔2〕 〔3〕2.如图 2 所示,假如 DE∥AB,那么∠A+______=180°,或∠B+_____=180...