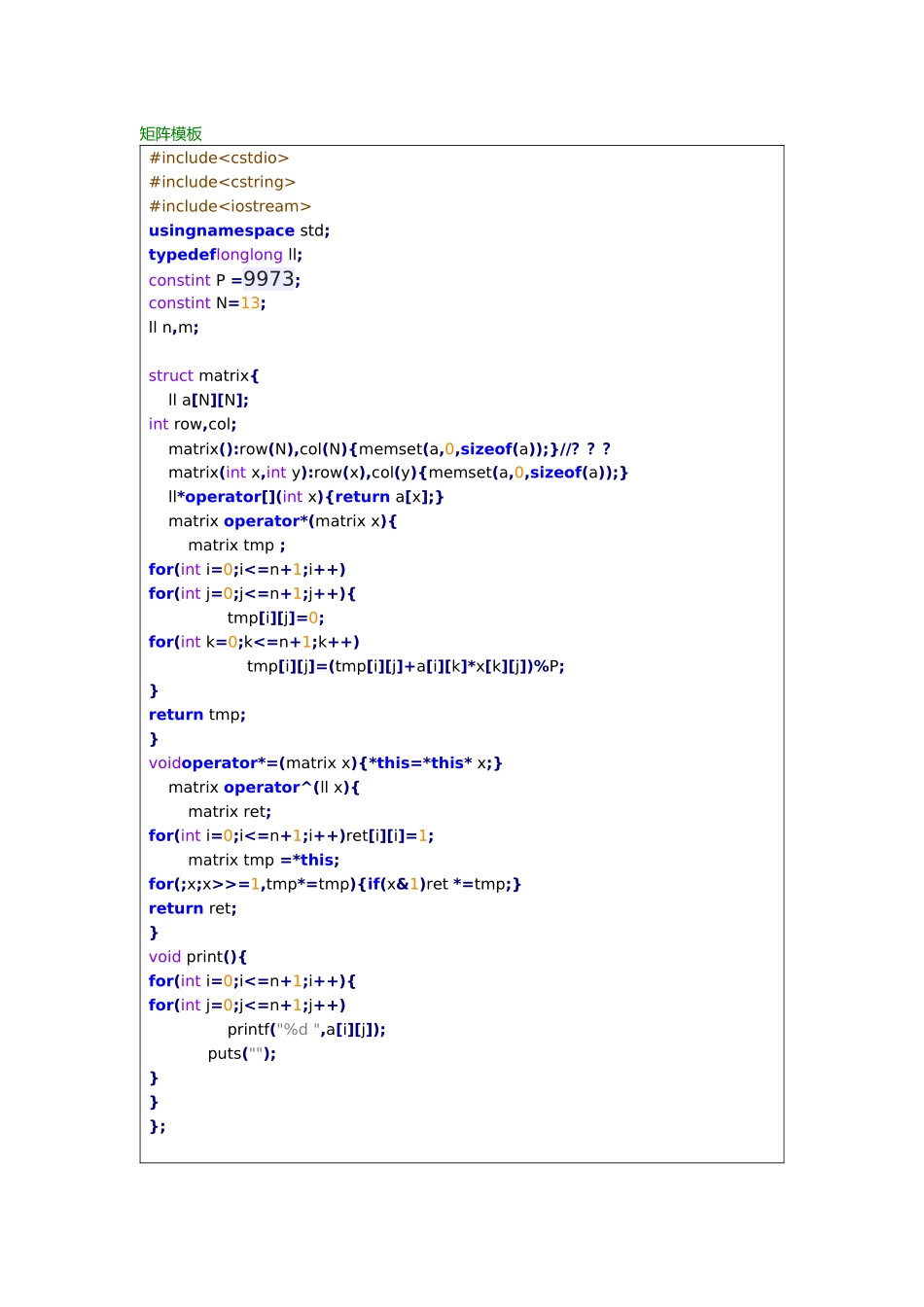
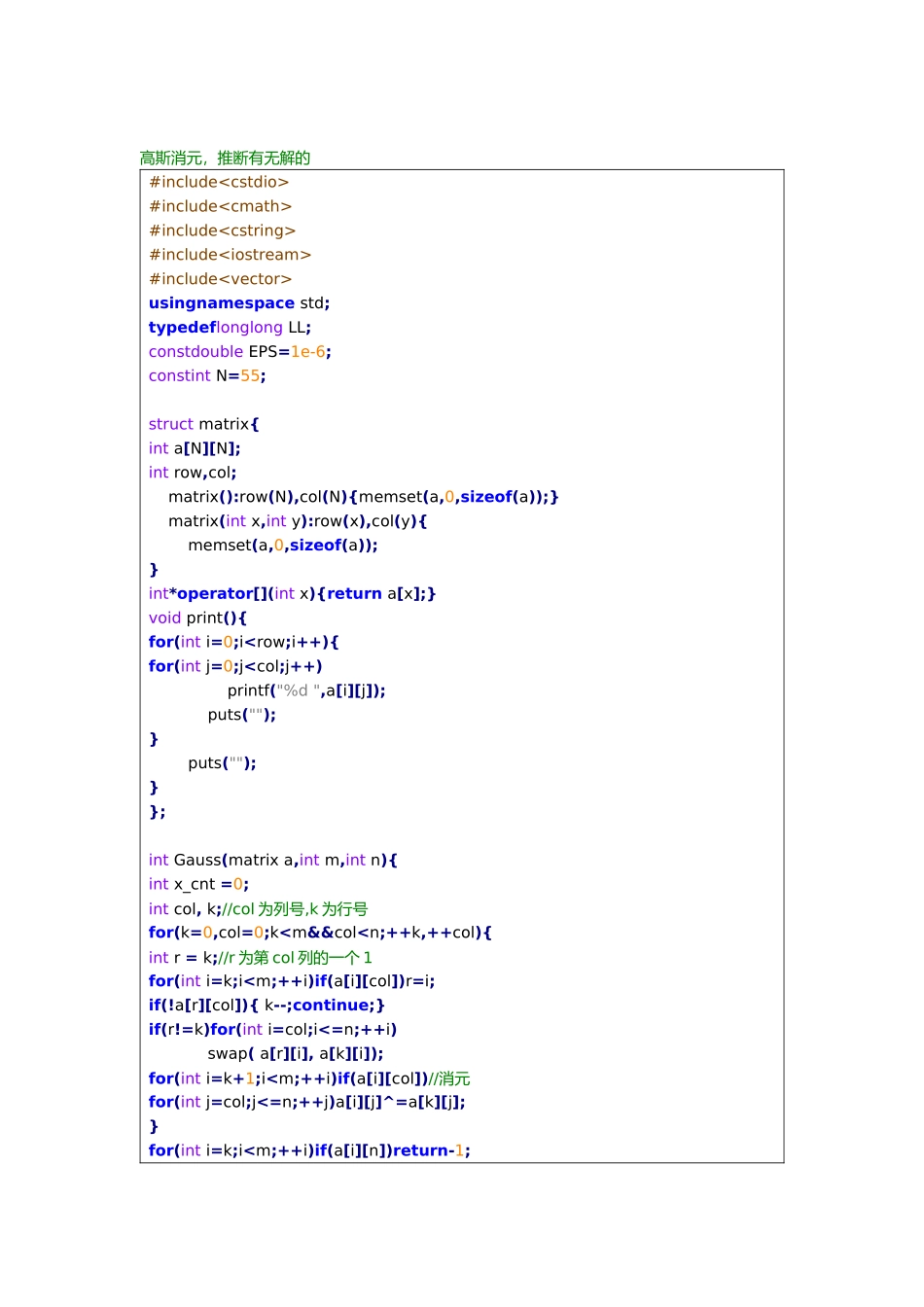
代码仓库目录:01.[数学方法]矩阵快速幂02.[数学方法]高斯消元(naïve 版)03.[数学方法]高斯消元(mid 版)04.[字符串啊]Manacher 算法(回文串)05.[字符串啊]KMP(字符串匹配)06.[数据结构]线段树(ZKW 单点修改)07.[数据结构]线段树(RMQ)08.[数据结构]线段树(区间加+赋值)09.[数据结构]Splay 树(未完全测试)////!!!!10.[数据结构]AVL 树(平衡树)11.[图论图论]最小生成树(prim)12.[图论图论]次小生成树13.[图论图论]最大流(Dinic)14.[图论图论]LCA+最大生成树(truck)15.[动态规划]背包 01,多重,完全矩阵模板#include #include#includeusingnamespace std;typedeflonglong ll;constint P =9973;constint N=13;ll n,m;struct matrix{ ll a[N][N];int row,col; matrix():row(N),col(N){memset(a,0,sizeof(a));}//??? matrix(int x,int y):row(x),col(y){memset(a,0,sizeof(a));} ll*operator[](int x){return a[x];} matrix operator*(matrix x){ matrix tmp ;for(int i=0;i<=n+1;i++)for(int j=0;j<=n+1;j++){ tmp[i][j]=0;for(int k=0;k<=n+1;k++) tmp[i][j]=(tmp[i][j]+a[i][k]*x[k][j])%P;}return tmp;}voidoperator*=(matrix x){*this=*this* x;} matrix operator^(ll x){ matrix ret;for(int i=0;i<=n+1;i++)ret[i][i]=1; matrix tmp =*this;for(;x;x>>=1,tmp*=tmp){if(x&1)ret *=tmp;}return ret;}void print(){for(int i=0;i<=n+1;i++){for(int j=0;j<=n+1;j++) printf("%d ",a[i][j]); puts("");}}};高斯消元,推断有无解的#include#include#include#include#includeusingnamespace std;typedeflonglong LL;constdouble EPS=1e-6;constint N=55;struct matrix{int a[N][N];int row,col; matrix():row(N),col(N){memset(a,0,sizeof(a));} matrix(int x,int y):row(x),col(y){ memset(a,0,sizeof(a));}int*operator[](int x){return a[x];}void print(){for(int i=0;i