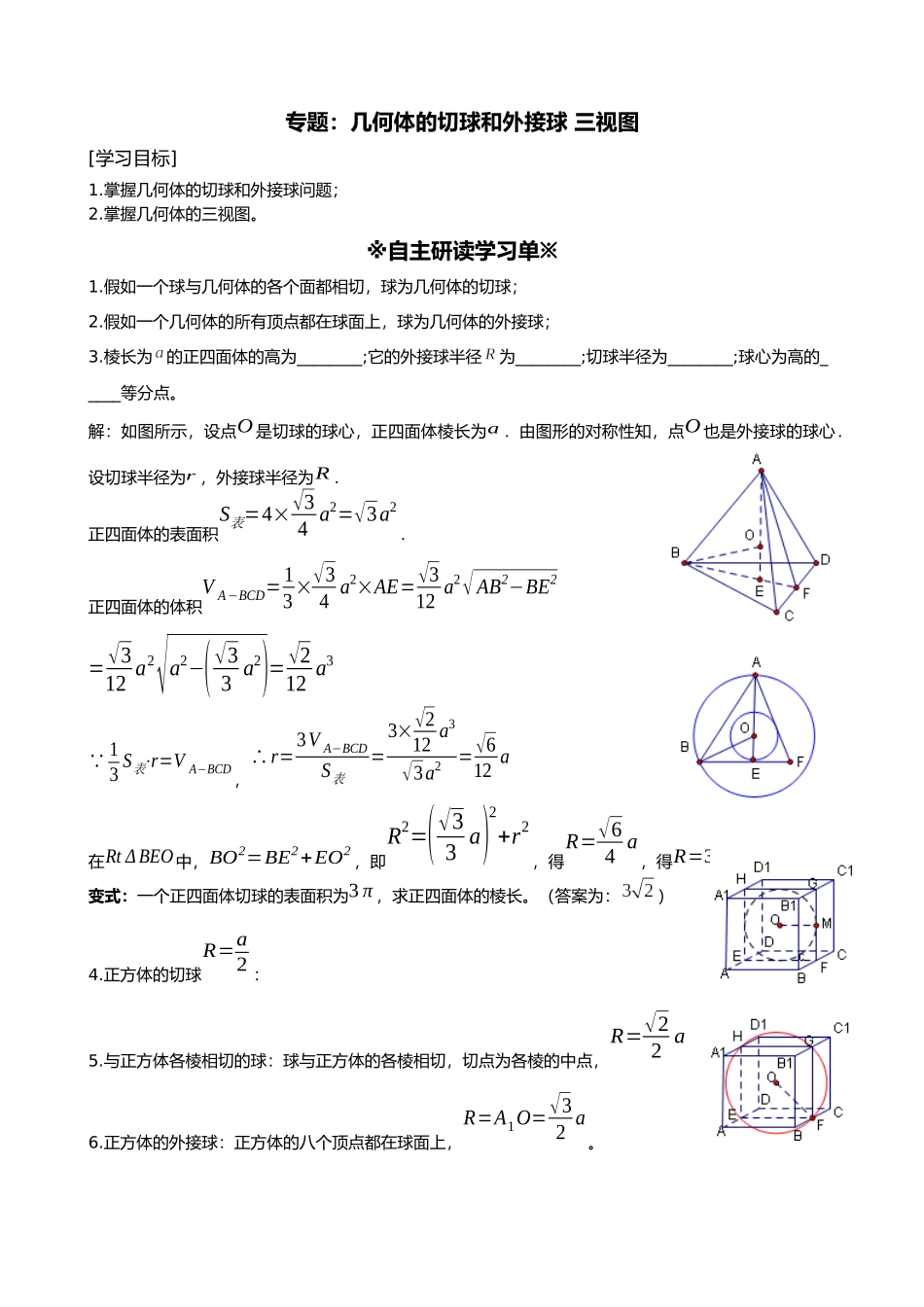
专题:几何体的切球和外接球 三视图[学习目标]1.掌握几何体的切球和外接球问题;2.掌握几何体的三视图。※自主研读学习单※1.假如一个球与几何体的各个面都相切,球为几何体的切球;2.假如一个几何体的所有顶点都在球面上,球为几何体的外接球;3.棱长为的正四面体的高为________;它的外接球半径为________;切球半径为________;球心为高的_____等分点。解:如图所示,设点O 是切球的球心,正四面体棱长为a .由图形的对称性知,点O 也是外接球的球心.设切球半径为r ,外接球半径为R .正四面体的表面积S表=4×√34 a2=√3a2.正四面体的体积V A−BCD=13 ×√34 a2×AE=√312 a2√ AB2−BE2=√312 a2√a2−(√33 a2)=√212 a3 13 S表⋅r=V A−BCD ,∴r=3V A−BCDS表=3×√212 a3√3a2=√612 a在Rt Δ BEO中,BO2=BE2+EO2 ,即R2=(√33 a)2+r2,得R=√64 a,得R=3r变式:一个正四面体切球的表面积为3 π ,求正四面体的棱长。(答案为:)4.正方体的切球R=a2 :5.与正方体各棱相切的球:球与正方体的各棱相切,切点为各棱的中点,R=√22 a6.正方体的外接球:正方体的八个顶点都在球面上,R=A1O=√32 a。变式:一棱长为2a的框架型正方体,放一能充气吹胀的气球,求当球与正方体棱适好接触但又不至于变形时的球的体积。(答案为)7.正棱柱的外接球,其球心定在上下底面中心连线的中点处,由球心、底面中心与底面一顶点构成的直角三角形便可得球半径。※合作探究学习单※题型一 几何体的切球和外接球例 1.正三棱锥的高为 1,底面边长为2√6,正三棱锥有一个球与其四个面相切.求球的表面积与体积.解:如图,球O 是正三棱锥P−ABC 的切球,O 到正三棱锥四个面的距离都是球的半径R .PH 是正三棱锥的高,即PH=1.E 是BC 边中点,H 在AE上,Δ ABC 的边长为2√6,∴HE=√36 ×2√6=√2. ∴PE=√3可以得到SΔ PAB=S Δ PAC=S Δ PBC=12 BC⋅PE=3√2. SΔ ABC=√34 (2√6)2=6√3由等体积法,V P−ABC=V O−PAB+V O−PAC+V O−PBC+V O−ABC∴13×6√3×1=13×3√2×R×3+ 13×6√3×R 得:R= 2√32√3+3=√6−2,∴S球=4 πR2=4 π (√6−2)2=8(5−2√6) π . ∴V 球=43 πR3=43 π(√6−2)3.例 2.求球与它的外切圆柱、外切等边圆锥的体积之比.分析:首先画出球与它的外切圆柱、等边圆锥,它们公共的轴截面,然后寻找几何体与几何体之间元素的关系.解:如图,等边Δ S...