数值分析上机实验报告

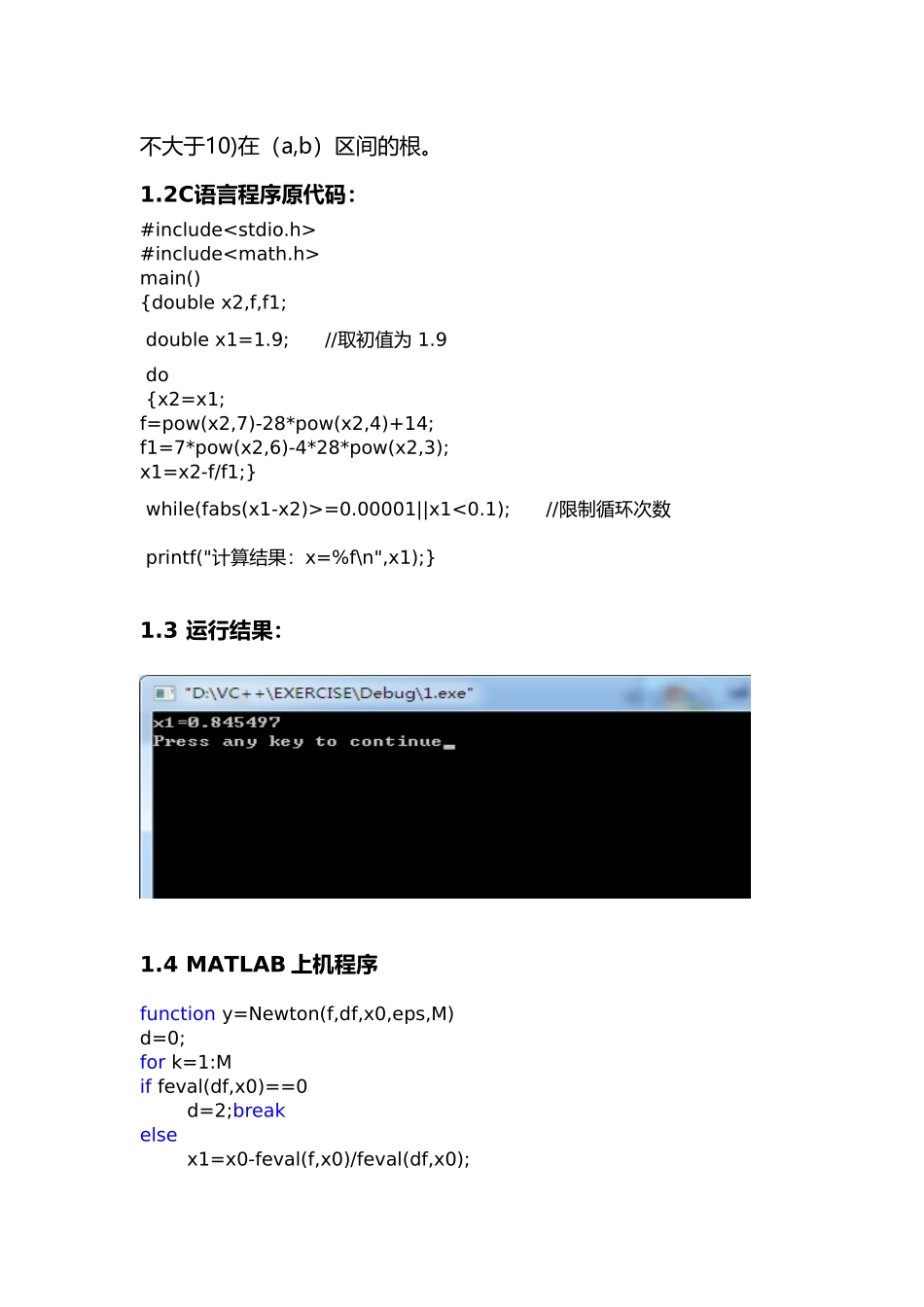
数值分析上机实验报告《数值分析》上机实验报告1.用 Newton 法求方程X7-X4+14=0在（0.1，1.9）中的近似根（初始近似值取为区间端点，迭代 6次或误差小于 0.00001）。1.1 理论依据：设函数在有限区间[a，b]上二阶导数存在，且满足条件令故以 1.9 为起点如此一次一次的迭代，逼近x的真实根。当前后两个的差<=ε时，就认为求出了近似的根。本程序用Newton法求代数方程(最高次数不大于10)在（a,b）区间的根。1.2C语言程序原代码：#include#includemain(){double x2,f,f1; double x1=1.9; //取初值为 1.9 do {x2=x1;f=pow(x2,7)-28*pow(x2,4)+14;f1=7*pow(x2,6)-4*28*pow(x2,3);x1=x2-f/f1;} while(fabs(x1-x2)>=0.00001||x1<0.1); //限制循环次数 printf("计算结果：x=%f\n",x1);}1.3 运行结果：1.4 MATLAB 上机程序function y=Newton(f,df,x0,eps,M)d=0;for k=1:Mif feval(df,x0)==0 d=2;breakelse x1=x0-feval(f,x0)/feval(df,x0);end e=abs(x1-x0); x0=x1;if e<=eps&&abs(feval(f,x1))<=eps d=1;breakendendif d==1 y=x1;elseif d==0 y='迭代 M 次失败';else y= '奇异'endfunction y=df(x)y=7*x^6-28*4*x^3;Endfunction y=f(x)y=x^7-28*x^4+14;End>> x0=1.9;>> eps=0.00001;>> M=100;>> x=Newton('f','df',x0,eps,M);>> vpa(x,7)1.5 问题讨论：1.使用此方法求方解，用误差来控制循环迭代次数，可以在误差允许的围得到比较理想的计算结果。此程序的不足之处是，所要求解的方程必须满足上述定理的四个条件，但是第二和第四个条件在计算机上比较难以实现。2.Newton 迭代法是一个二阶收敛迭代式，他的几何意义 Xi+1 是 Xi 的切线与 x 轴的交点,故也称为切线法。它是平方收敛的，但它是局部收敛的，即要求初始值与方程的根充分接近，所以在计算过程中需要先确定初始值。3.本题在理论依据部分，讨论了区间(0.1,1.9)两端点是否能作为 Newton迭代的初值，结果发现 0.1 不满足条件，而 1.9 满足，能作为初值。另外，该程序简单，只有一个循环，且为顺序结构，故采纳 do-while 循环。当然也可以选择 for 和 while 循环。2.已知函数值如下表：x12345f(x)00.693147181.09861231.38629441.6094378x678910f(x)1.79175951.94591012.0794452.19722462.3025851f’(x)f’(1)=1f’(10)=0.1试用三次样条插值求 f(4.563)与 f’(4.563)的近似值。2.1 理论依据这里 ，所以只要求出，...