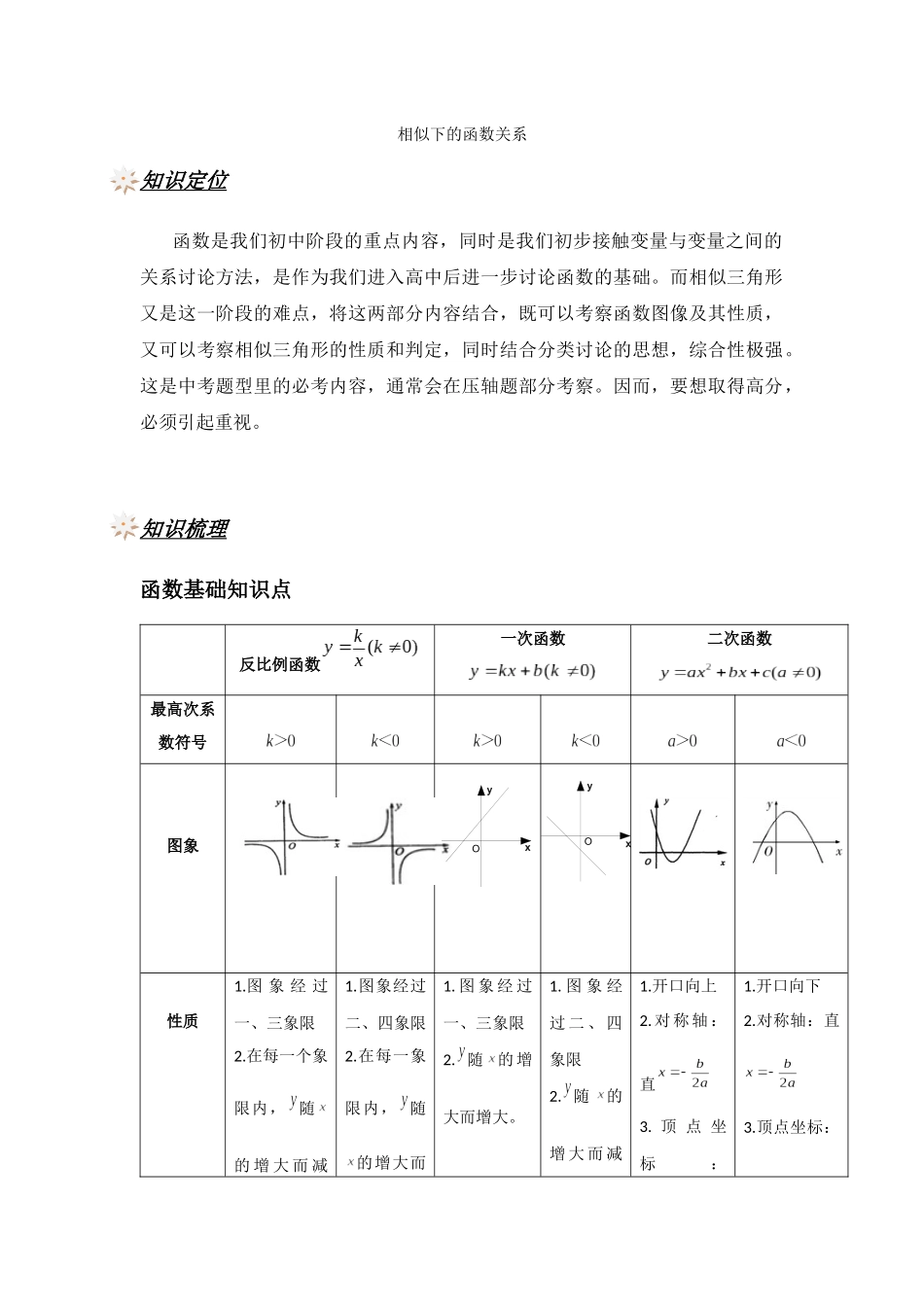
相似下的函数关系知识定位函数是我们初中阶段的重点内容,同时是我们初步接触变量与变量之间的关系讨论方法,是作为我们进入高中后进一步讨论函数的基础。而相似三角形又是这一阶段的难点,将这两部分内容结合,既可以考察函数图像及其性质,又可以考察相似三角形的性质和判定,同时结合分类讨论的思想,综合性极强。这是中考题型里的必考内容,通常会在压轴题部分考察。因而,要想取得高分,必须引起重视。知识梳理函数基础知识点反比例函数一次函数二次函数最高次系数符号图象性质1.图 象 经 过一、三象限2.在每一个象限内,随的 增 大 而 减1.图象经过二、四象限2.在每一象限内,随的增大而1. 图 象 经 过一、三象限2. 随的增大而增大。1. 图 象 经过 二 、 四象限2. 随的增 大 而 减1.开口向上2. 对 称 轴 :直3. 顶 点 坐标:1.开口向下2.对称轴:直3.顶点坐标:yxOyxO小。增大。小。函数综合题目考点分析:1.求解函数解析式,以二次函数为主;2.求解相关点的坐标,二次函数中一般考察求对称轴、顶点坐标;3.以函数为背景,考察相似、等腰、相切、平行四边形、面积等相关知识点;该类题型综合性很强,需要及时画图观察。掌握相似三角形的基本图形A.字形B.八字形C.一线三等角D.一线三直角E.母子三角形二次函数背景下相似三角形的解题方法和策略:1.根据题意,先求解相关点的坐标和相关线段的长度;2.待定系数法求解相关函数的解析式;3.相似三角形中,注意寻找不变的量和相等的量(角和线段);4.当三角形的三边不能用题目中的未知量表示时,注意利用相似三角形的转化求解;5.根据题目条件,注意快速、正确画图,用好数形结合思想;6.注意利用好二次函数的对称性;7.利用几何定理和性质或者代数方法建立方程求解都是常用方法。例题精讲【题目】已知:如图,抛物线y= 14 x2+ 12 x−2与x、 y 轴分别相交于、两点,将△AOB 绕着点逆时针旋 90°到△,且抛物线过点、。(1)求、两点的坐标;(2)求抛物线的解析式;(3)点在 轴上,若以为顶点的三角形与△A' B' B 相似,求点的坐标。 B'A'OBAyx【题目】已知:如图,抛物线的顶点为点,与 y 轴相交于点,直线 y=ax+3 与 y 轴也交于点,矩形的顶点 B 在此抛物线上,矩形面积为 12。(1)求该抛物线的对称轴;(2)⊙P 是经过 A、B 两点的一个动圆,当⊙P 与 y 轴相交,且在 y 轴上两交点的距离为 4 时,求圆心的坐标;(3)若线段...