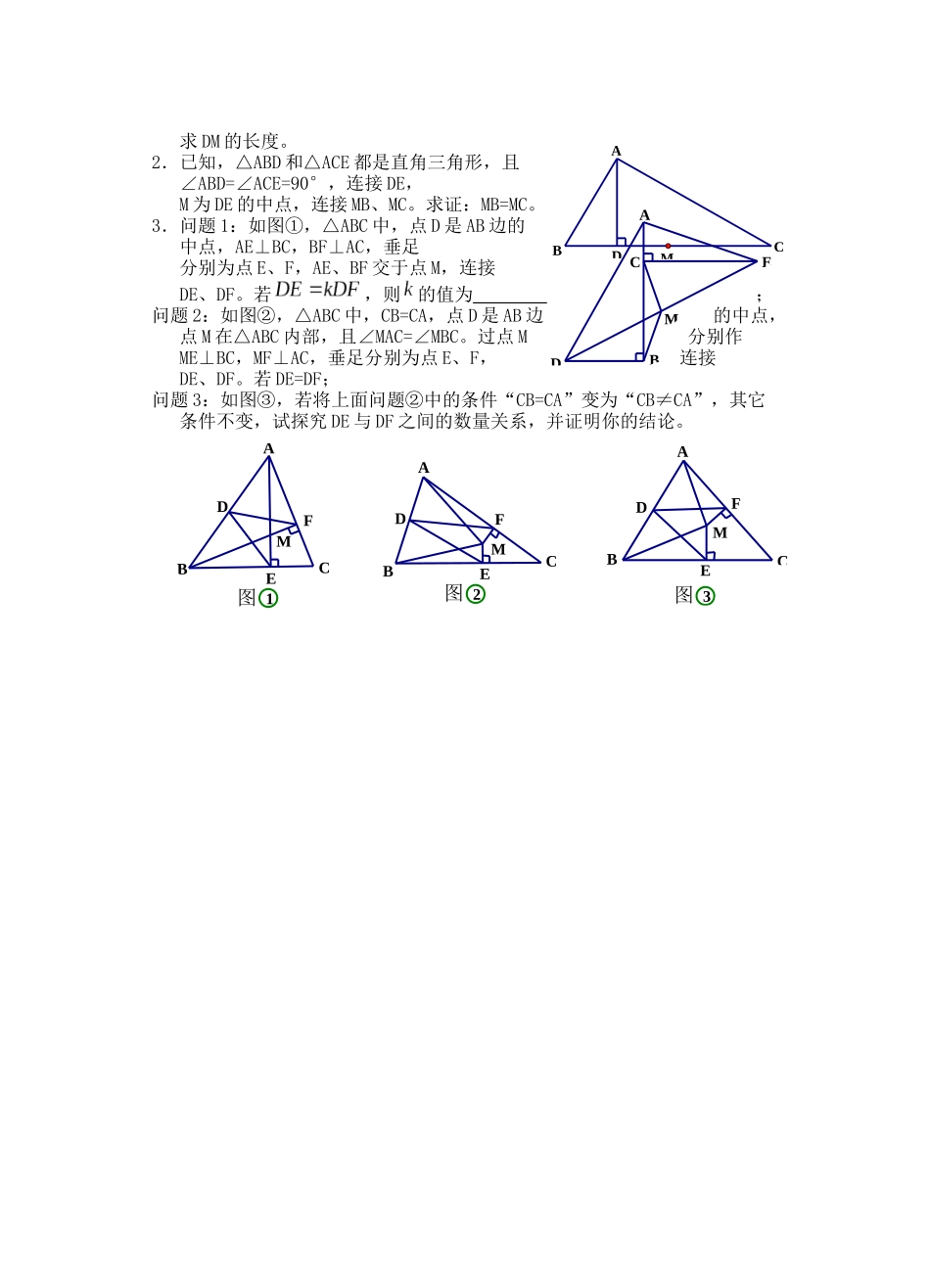
第八章 中点四大模型模型分析如图①,AD 是△ABC 的中线,延长 AD 至点 E 使 DE=AD,易证:△ADC≌△EDB(SAS)。如图②,D 是 BC 中点,延长 FD 至点 E 使 DE=FD,易证:△FDB≌△FDC(SAS)。当遇见中线或者中点的时候,可以尝试倍长中线或类中线,构造全等三角形,目的是对已知条件中的线段进行转移。模型实例例 1.如图,已知在△ABC 中,AD 是 BC 边上的中线,E 是 AD 上一点,连接 BE 并延长 AC 于点 F,AF=EF。求证:AC=BE。热搜精练1.如图,在△ABC 中,AB=12,AC=20,求 BC 边上中线 AD 的范围。2.如图,在△ABC 中,D 是 BC 的中点,DM⊥DN,假如。 求证:。模型 2 已知等腰三角形底边中点,可以考虑与顶点连接用“三线合一”模型分析等腰三角形中有底边中点时,常作底边的中线,利用等腰三角形“三线合一”的性质得到角相等或边相等,为解题制造更多的条件,当看见等腰三角形的时候,就应想到:“边等、角等、三线合一”。模型实例例 1.如图,在△ABC 中,AB=AC-5,BC=6,M 为 BC 的中点,MN⊥AC 于点 N, 求 MN 的长度。热搜精练1.如图,在△ABC 中,AB=AC,D 是 BC 的中点,AE⊥DE,AF⊥DF,且 AE=AF。 求证:∠EDB=∠FDC。2.已知 Rt△ABC 中,AC=BC,∠C=90°,D 为 AB边的中点,∠EDF=90°, ∠EDF 绕点 D 旋转,它的两边分别交 AC、CB(或它们的延长线)于 E、F。(1)当∠EDF 绕点 D 旋转到 DE⊥AC 于 E 时(如图①),求证:;(2)当∠EDF 绕点 D 旋转到 DE 和 AC 不垂直时,在图②和图③这两种情况下, 上述结论是否成立?若成立,请给予证明;若不成立,、、 又有怎样的数量关系?请写出你的猜想,不需证明。模型 3 已知三角形一边的中点,可以考虑中位线定理模型分析FDBACENMDBACNMBACFDBACE构造中位线取另一边中点DBACDBACE在三角形中,假如有中点,可构造三角形的中位线,利用三角形中位线的性质定理:DE∥BC,且来解题,中位线定理既有线段之间的位置关系又有数量关系,该模型可以解决相等,线段之间的倍半、相等及平行问题。。模型实例例 1.如图,在四边形 ABCD 中,AB=CD,E、F 分别是 BC、AD 的中点,连接 EF 并延长,分别与 BA、CD 的延长线交于点 M、N。 求证:∠BME=∠CNE。热搜精练1.(1)如图①,BD、CE 分别是△ABC 的外角平分,过点 A作AD⊥BD、AE⊥CE,垂足分别为 D、E,连接 DE。求证:DE∥B...