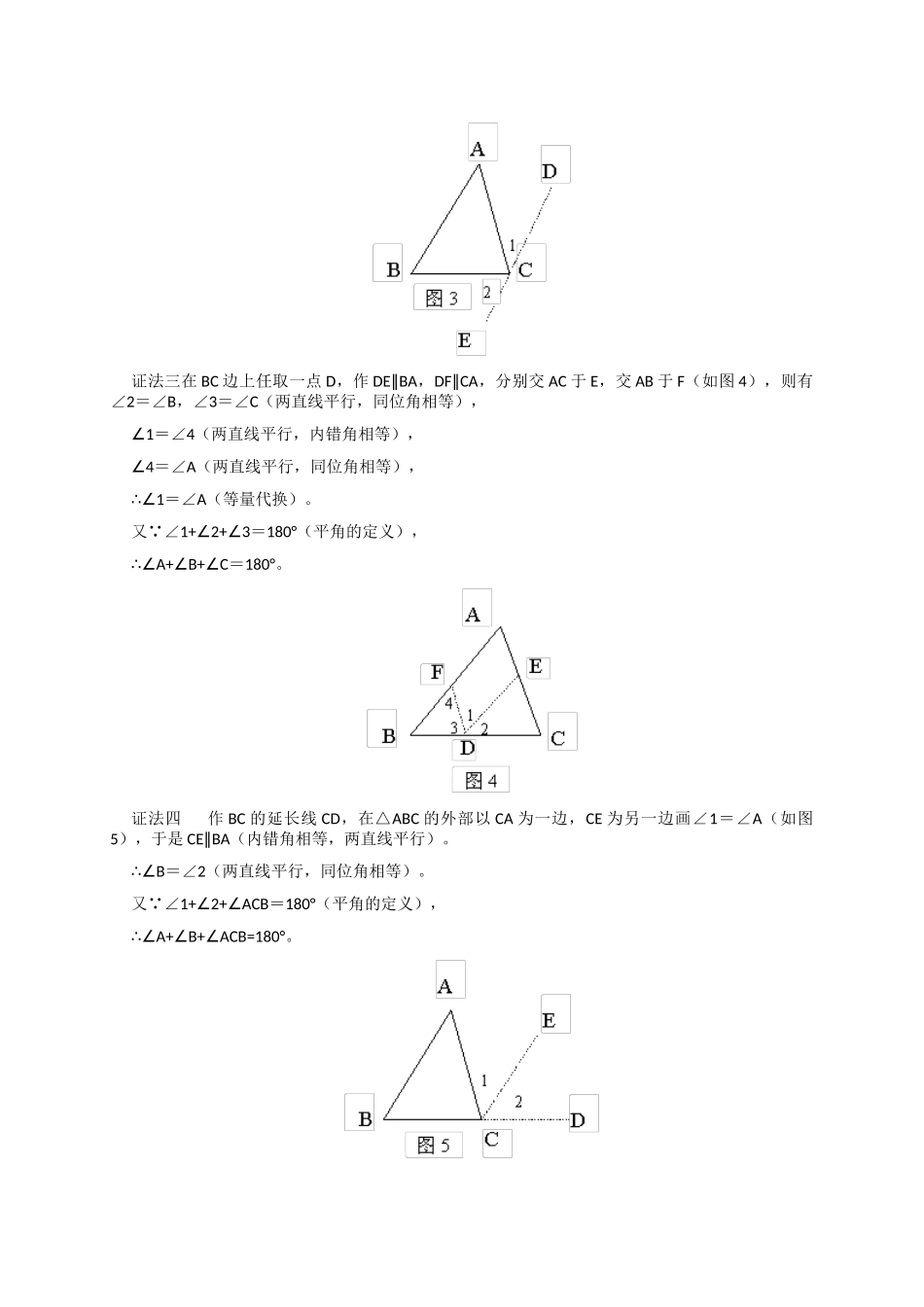
三角形内角和定理证明中化归思想的渗透所谓化归思想,就是在面临新问题时,总企图将它转化归结为已经解决了的问题或者比较熟悉的问题来解决。初中数学尤其是几何教学中,很多问题都可以用运化归思想来解决。三角形内角和定理 三角形三个内角的和等干 180°。已知:△ABC(如图 1)。求证:∠A+B+C=180°∠∠。三角形内角和定理有多种证明方法,那么,这些证法都是怎样想到的呢?我们下面来作一下分析,思路一 要证明三角形的三个内角之和等于 180°,联想到平角的大小是 180°。因此,便设法将三角形的三个内角拼成一个平角,为此,用辅助线构造出一个平角,再用辅助线(平行线)“移动”内角,将其集中起来,或用其它方法将其集中起来,这就是“拼角”的思路。“移动内角(或用其它方法)”把三角形的三个内角拼成一个平角根据这个思路,可设计出多种证法,证法如下:证法一 延长边 BC,CD 是延长线,并过顶点 C 作 CE BA∥(如图 2),则∠1=A∠ (两直线平行,内错角相等),∠2=B∠ (两直线平行,同位角相等)。又 ∠1+2+ACB∠∠=180° (平角的定义),A+B+ACB∴∠∠∠=180°。证法二 过顶点 C 作 DE AB∥(如图 3),则∠1=∠A,∠2=∠B(两直线平行,内错角相等)。又 ∠1+ACB+2∠∠ =180°(平角的定义),A+ACB+B∴∠∠∠ =180°证法三在 BC 边上任取一点 D,作 DE BA∥,DF CA∥,分别交 AC 于 E,交 AB 于 F(如图 4),则有∠2=∠B,∠3=∠C(两直线平行,同位角相等),1∠ =∠4(两直线平行,内错角相等),4∠ =∠A(两直线平行,同位角相等),1∴∠ =∠A(等量代换)。又 ∠1+2+3∠∠ =180°(平角的定义),A+B+C∴∠∠∠ =180°。 证法四 作 BC 的延长线 CD,在△ABC 的外部以 CA 为一边,CE 为另一边画∠1=∠A(如图5),于是 CE BA∥(内错角相等,两直线平行)。B∴∠ =∠2(两直线平行,同位角相等)。又 ∠1+2+ACB∠∠=180°(平角的定义),A+B+ACB=180°∴∠∠∠。证法五 在△ABC 的内部任取一点 D,连结 AD、BD,并延长分别交边 BC、AC 于点 E、F,再连结 CD(如图 6),则有∠7=1+2∠∠ ,∠8=∠3+4∠ ,∠9=5+6∠∠ (三角形的任何一个外角等于和它不相邻的两个内角的和)。又 ∠7+8+9=180° ∠∠(平角的定义),1+2+3+4+5+6=180°∴∠∠∠∠∠∠。即∠BAC+ABC+ACB=180°∠∠。思路二 我们知道,平行线的同旁内角之和...