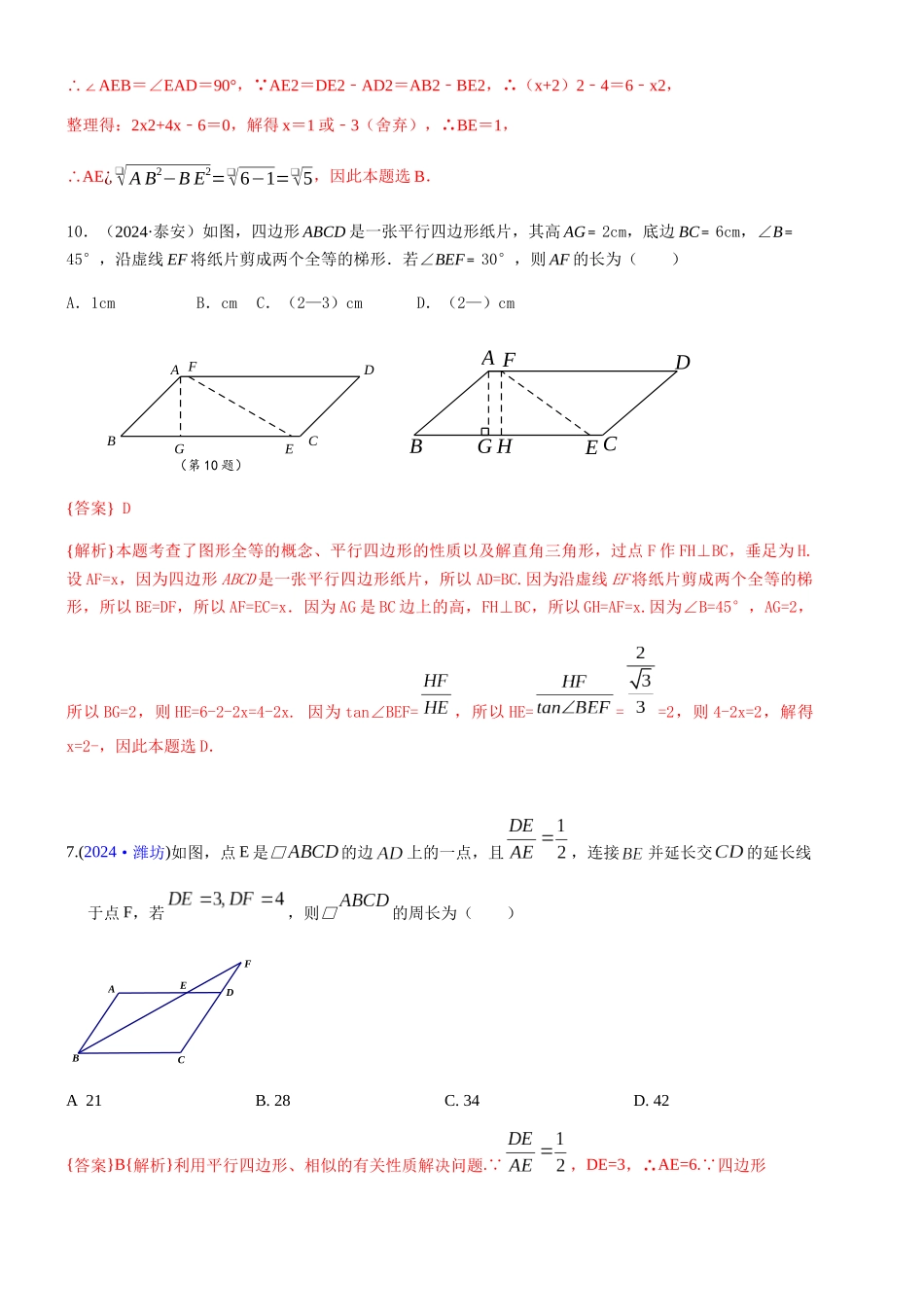
一、选择题5.(2024·温州)如图,在△ABC 中,∠A=40°,AB=AC,点 D 在 AC 边上,以 CB,CD 为边作□BCDE,则∠E 的度数为 A.40° B.50° C.60° D.70°{答案}D{解析}本题考查了等腰三角形的性质以及平行四边形的性质,由∠A=40°,AB=AC,求得∠C=70°,又因为四边形 BCDE 是平行四边形,所以∠E=∠C=70°,因此本题选 D.7.(2024·衡阳)如图,在四边形 ABCD 中,对角线 AC 和 BD 相交于点 O.下列条件不能推断四边形 ABCD 是平行四边形的是 ( ) A. AB∥DC ,AD∥BC B. AB= DC,AD= BC C. AB∥DC,AD =BC D.OA= OC,OB =OD (第 7 题图){答案}C{解析}本题考查了平行四边形的判定.注意掌握举反例的解题方法是解本题的关键. ABDC∥ ADBC∥,∴四边形 ABCD 是平行四边形,故 A 选项能判定这个四边形是平行四边形; AB=DC AD=BC,∴四边形 ABCD 是平行四边形,故 B 选项能判定这个四边形是平行四边形;、 ABDC∥ AD=BC,∴四边形 ABCD 是平行四边形或等腰梯形,故 C 选项不能判定这个四边形是平行四边形. AO=CO BO=DO,∴四边形 ABCD 是平行四边形,故 D 选项能判定这个四边形是平行四边形;故选 C.12.(2024 自贡)如图,在平行四边形 ABCD 中,AD=2,AB¿ ❑√6,∠B 是锐角,AE⊥BC 于点 E,F 是 AB的中点,连结 DF、EF.若∠EFD=90°,则 AE 长为( )A.2B.❑√5C.3❑√22D.3❑√32{答案} B.{解析}本题考查了平行四边形、全等三角形、勾股定理、一元二次方程等知识.解:如图,延长 EF 交 DA 的延长线于 Q,连接 DE,设 BE=x. 四边形 ABCD 是平行四边形,∴DQ BC∥,∴∠Q=∠BEF,AF =FB,∠AFQ=∠BFE,∴△QFAEFB≌△(AAS),∴AQ=BE=x,EFD ∠=90°,∴DFQE⊥,∴DQ=DE=x+2, AEBC⊥,BC AD∥,∴AEAD⊥,EDCBAAEB∴∠=∠EAD=90°, AE2=DE2AD2﹣=AB2BE2﹣,∴(x+2)24﹣ =6x2﹣,整理得:2x2+4x6﹣ =0,解得 x=1 或﹣3(舍弃),∴BE=1,AE∴¿❑√ A B2−B E2=❑√6−1=❑√5,因此本题选 B.10.(2024·泰安)如图,四边形 ABCD 是一张平行四边形纸片,其高 AG﹦2cm,底边 BC﹦6cm,∠B﹦45°,沿虚线 EF 将纸片剪成两个全等的梯形.若∠BEF﹦30°,则 AF 的长为( )A.1cmB.cmC.(2—3)cmD.(2—)cm ABCDEFGE CFHABDG{答案} D{解析}本题考查了图形全等的概...