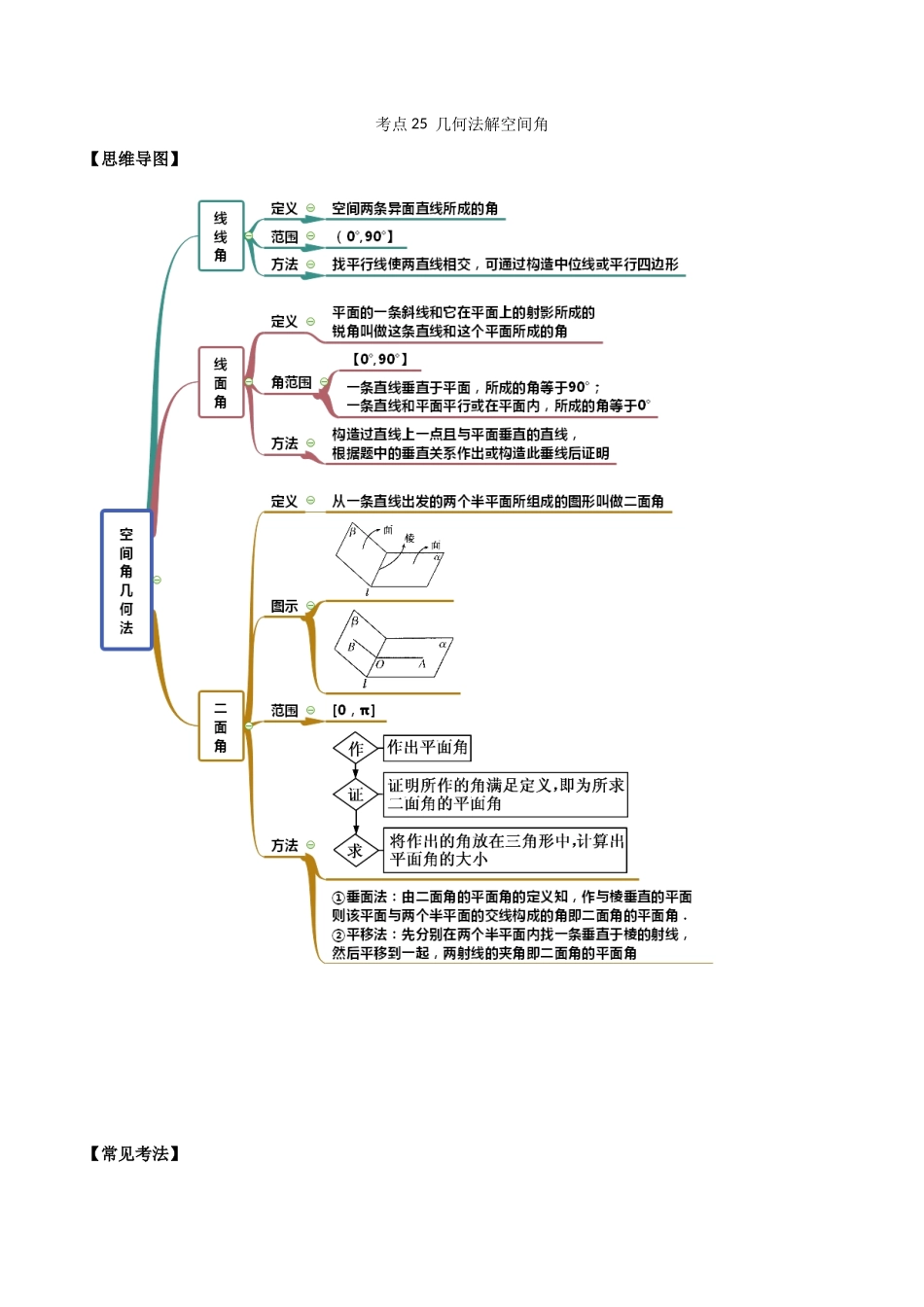
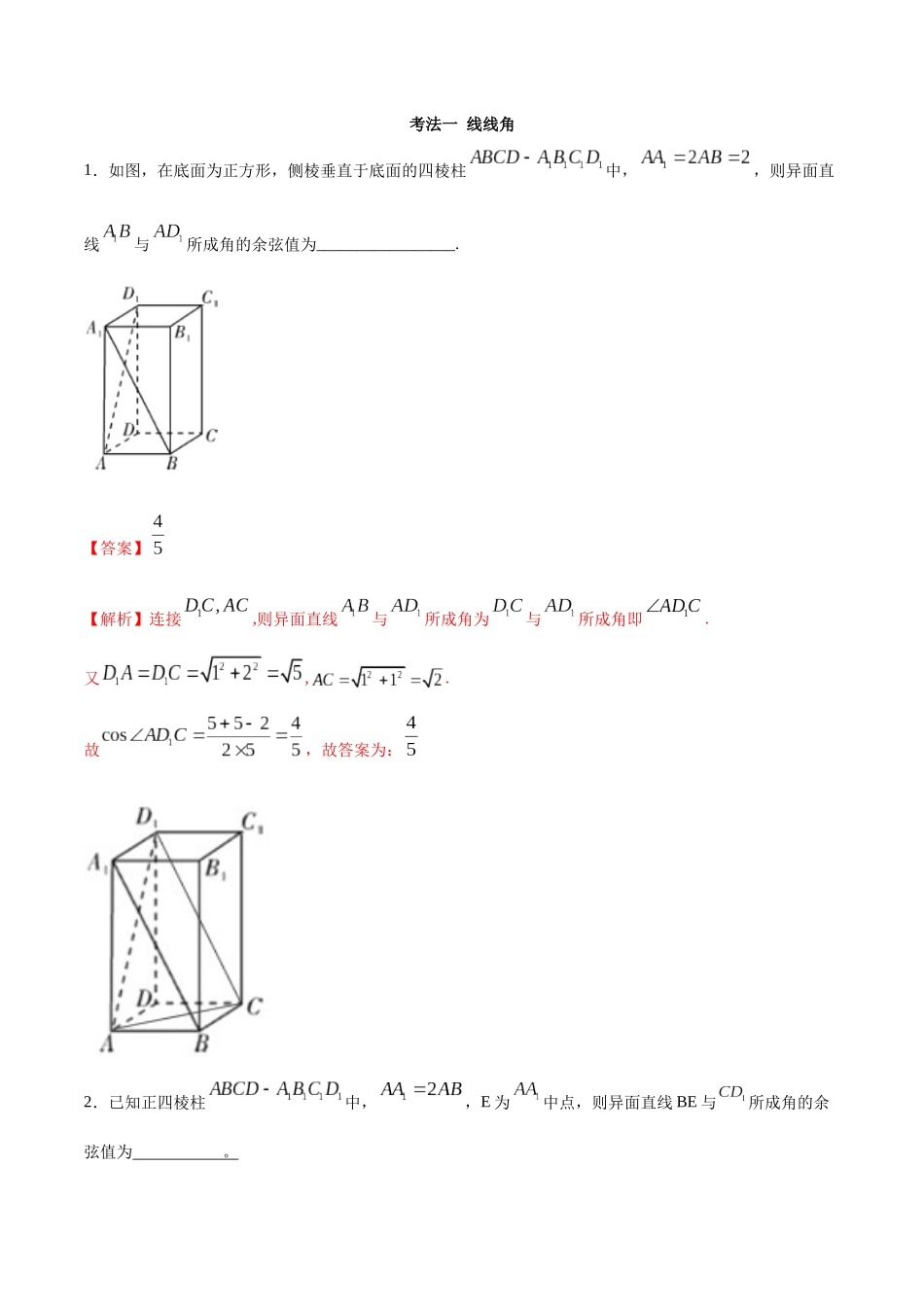
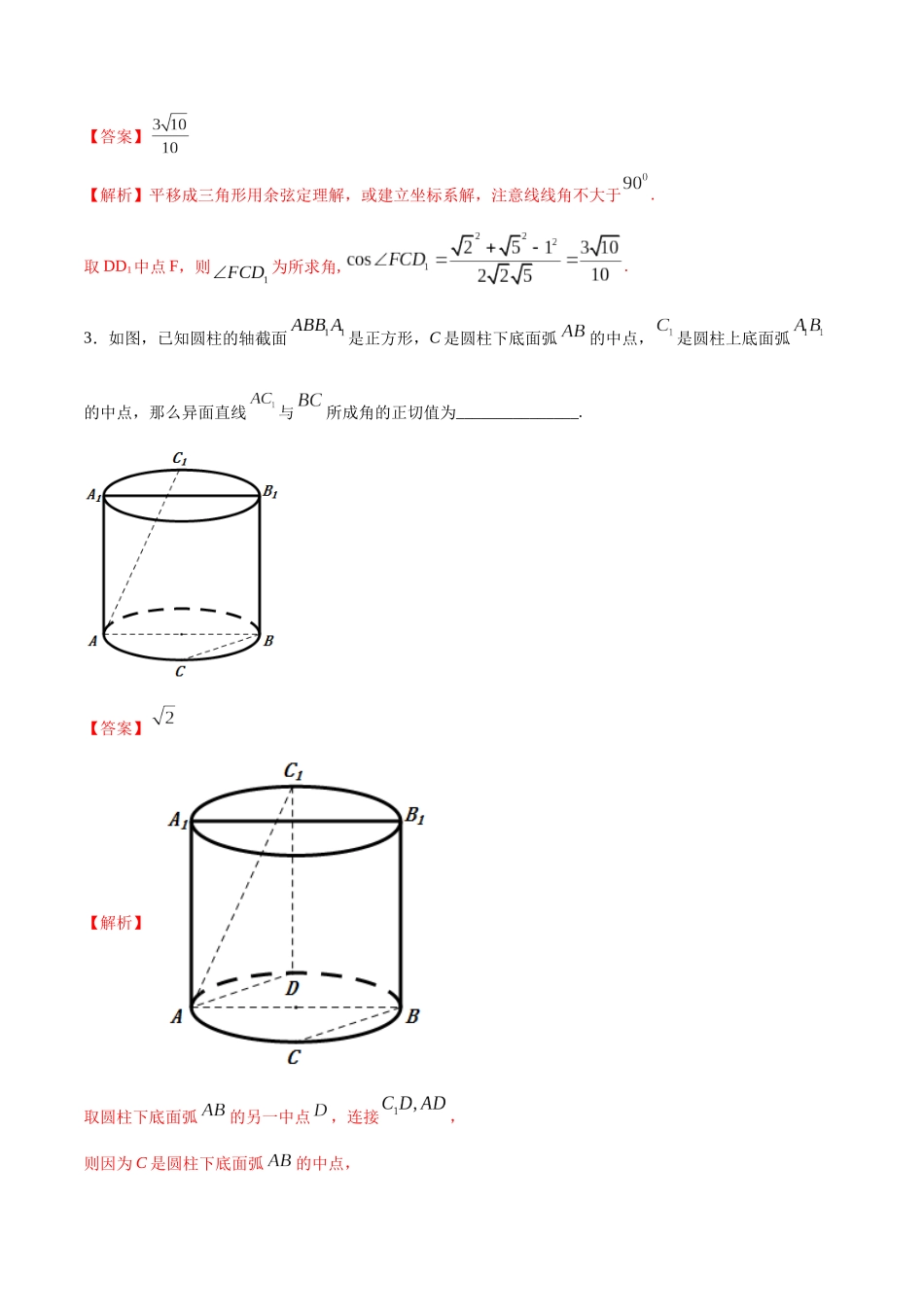
考点 25 几何法解空间角【思维导图】【常见考法】考法一 线线角1.如图,在底面为正方形,侧棱垂直于底面的四棱柱中,,则异面直线与所成角的余弦值为_________________.【答案】【解析】连接,则异面直线与所成角为与所成角即.又,.故,故答案为:2.已知正四棱柱中,,E 为中点,则异面直线 BE 与所成角的余弦值为 。【答案】【解析】平移成三角形用余弦定理解,或建立坐标系解,注意线线角不大于.取 DD1中点 F,则为所求角, .3.如图,已知圆柱的轴截面是正方形,C 是圆柱下底面弧的中点,是圆柱上底面弧的中点,那么异面直线与所成角的正切值为_______________.【答案】【解析】取圆柱下底面弧的另一中点,连接,则因为 C 是圆柱下底面弧的中点,所以,所以直线与所成角等于异面直线与所成角.因为是圆柱上底面弧的中点,所以圆柱下底面,所以.因为圆柱的轴截面是正方形,所以,所以直线与所成角的正切值为.所以异面直线与所成角的正切值为.故答案为:.4.如图,是圆的直径,点是弧的中点,分别是的中点,求异面直线与所成的角 。【答案】【解析】是圆的直径,. 点是弧的中点,.在中,分别为的中点,,与所成的角为.故答案为:5.已知三棱柱的侧棱与底面边长都相等,在底面上的射影为的中点,则异面直线与所成的角的余弦值为 。【答案】【解析】如图,设的中点为,连接、、,易知即为异面直线与所成的角(或其补角)设三棱柱的侧棱与底面边长均为 1,则,,,由余弦定理,得考法二 线面角1.如图,在正方体中,与平面所成角的余弦值是 .【答案】【解析】如图,连接交于,则,又正方体中平面A1B1C1D1,平面A1B1C1D1,∴,而,∴平面,∴是直线与平面所成角,此角大小为 45°,余弦值为.2.如图,在直三棱柱中,为的中点.若,,求与平面所成角的正弦值 。【答案】【解析】过点作于点,如图, 三棱柱为直三棱柱,∴平面. 平面,∴. ,为的中点,∴.又,∴平面, 平面,∴.又,,∴平面,∴为与平面所成的角设,则,,∴.3.如图,已知四棱锥的侧棱底面,且底面是直角梯形,,,,,,点在棱上,且.(1)证明:平面.(2)求直线与平面所成角的正弦值.【答案】(1)证明见解析;(2).【解析】(1)证明:取的三等分点,且,连接,,因为,,所以,且,因为,,所以,且,所以四边形为平行四边形,所以,因为平面,平面,所以平面;(2)过点作,垂足为,连接,因为平面,所以,所以平面,则为直线与平面所成的角,由题意可得...