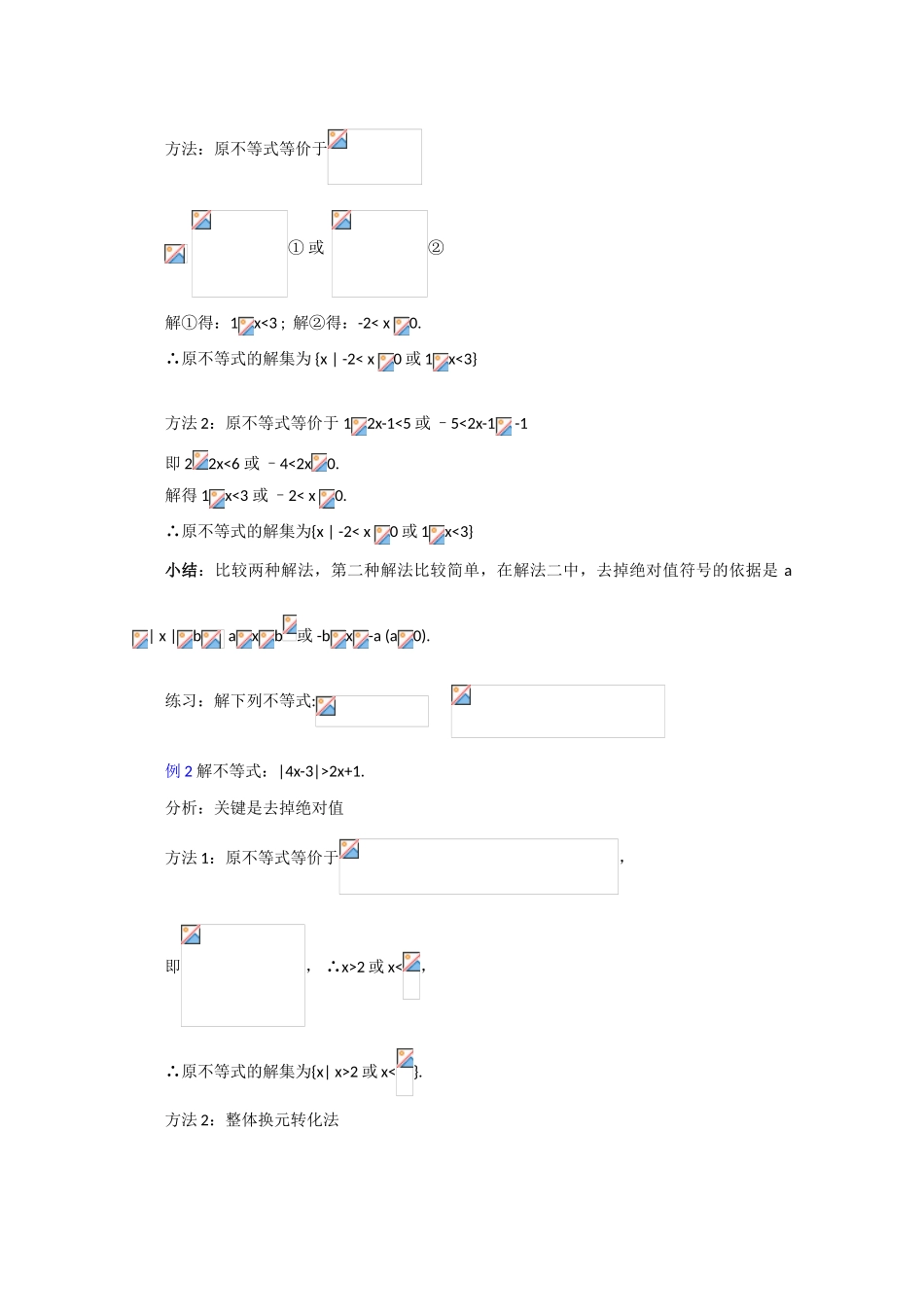
课 题:1.4 绝对值不等式的解法(2)教学目的:(1)巩固与型不等式的解法,并能熟练地应用它解决问题;掌握分类讨论的方法解决含多个绝对值的不等式以及含参数的不等式;(2)培养数形结合的能力,分类讨论的思想,培养通过换元转化的思想方法,培养抽象思维的能力;(3)激发学习数学的热情,培养勇于探索的精神,勇于创新精神,同时体会事物之间普遍联系的辩证思想教学重点:分类讨论的方法解决含多个绝对值的不等式以及含参数的不等式教学难点:如何正确分类与分段,简单的参数问题授课类型:新授课课时安排:1 课时教 具:多媒体、实物投影仪内容分析:(略) 教学过程: 一、复习引入:与型不等式与型不等式的解法与解集不等式的解集是;不等式的解集是不等式的解集为 ;不等式的解集为 二、讲解范例:例 1 解不等式 1 | 2x-1 | < 5.分析:怎么转化?怎么去掉绝对值?方法:原不等式等价于 ① 或 ②解①得:1x<3 ; 解②得:-2< x 0.∴原不等式的解集为 {x | -2< x 0 或 1x<3}方法 2:原不等式等价于 12x-1<5 或 –5<2x-1 -1即 22x<6 或 –4<2x0.解得 1x<3 或 –2< x 0.∴原不等式的解集为{x | -2< x 0 或 1x<3}小结:比较两种解法,第二种解法比较简单,在解法二中,去掉绝对值符号的依据是 a| x |b axb或 -bx-a (a0).练习:解下列不等式: 例 2 解不等式:|4x-3|>2x+1.分析:关键是去掉绝对值方法 1:原不等式等价于,即, ∴x>2 或 x<,∴原不等式的解集为{x| x>2 或 x<}.方法 2:整体换元转化法分析:把右边看成常数 c,就同一样 |4x-3|>2x+14x-3>2x+1 或 4x-3<-(2x+1) x>2 或 x<,∴原不等式的解集为{x| x>2 或 x<}.例 3 解不等式:|x-3|-|x+1|<1.分析:关键是去掉绝对值方法 1:零点分段讨论法(利用绝对值的代数定义)① 当时,∴ ∴ 4<1 ② 当时∴,∴③ 当时-4<1 ∴综上 原不等式的解集为也可以这样写:解 : 原 不 等 式 等 价 于 ①或 ②或 ③,解①的解集为 φ,②的解集为{x|}.方法 2:数形结合从形的方面考虑,不等式|x-3|-|x+1|<1 表示数轴上到 3 和-1 两点的距离之差小于 1 的点∴原不等式的解集为{x|x>}.练习:解不等式:| x+2 | + | x | >4.分析 1:零点分段讨论法解法 1:①当 x-2 时,不等式化为 -(x+2)- x > 4 即 x<-3. 符合题义 ② 当...