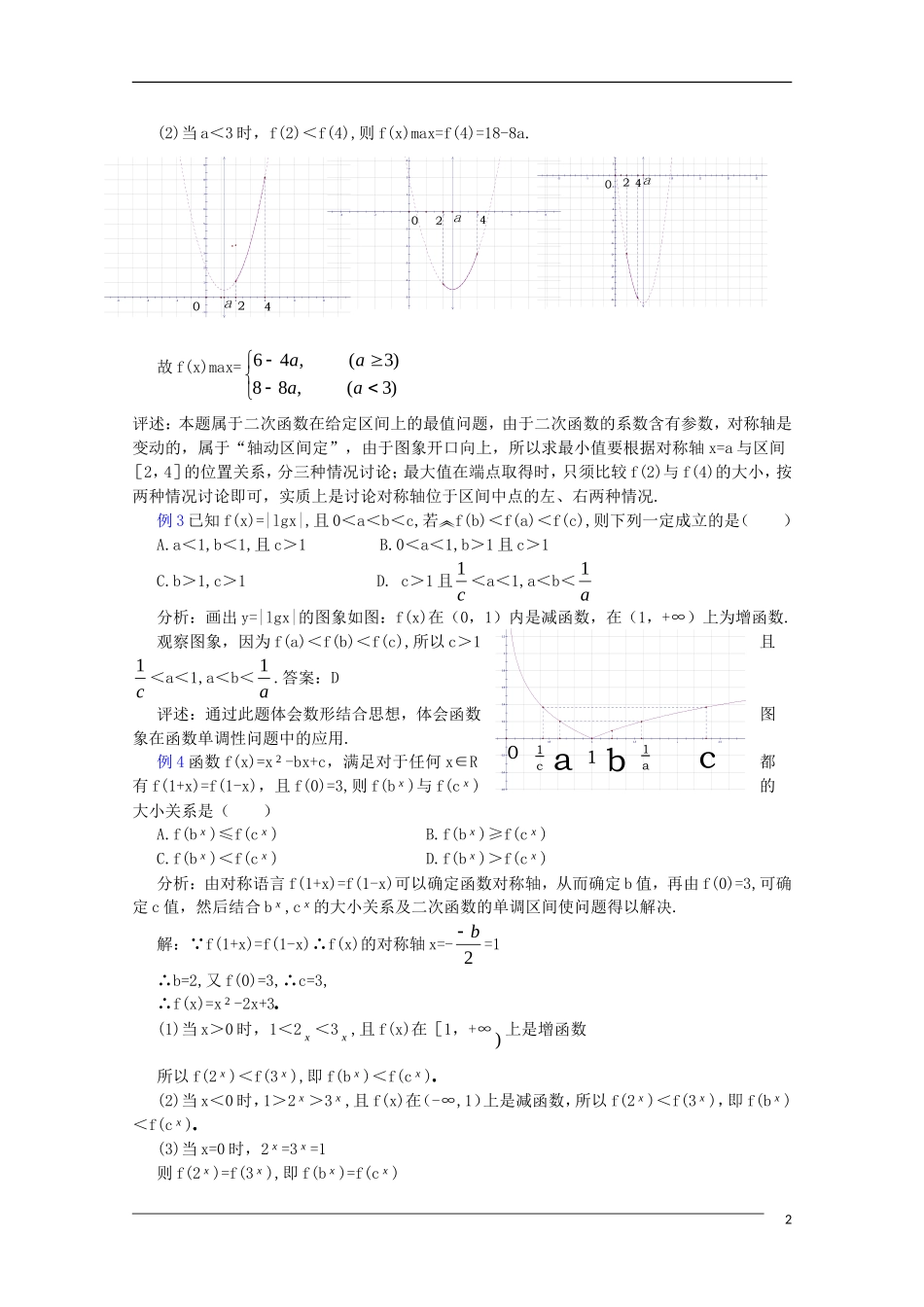
课 题:函数复习小结(2)教学目的: 1.熟悉并掌握函数的对称语言.2.进一步熟悉二次函数性质及其应用.3.把握数形结合的特征和方法.4.能够应用函数思想解题.5.了解与函数有关的数学模型.教学重点:数形结合的特征与方法教学难点:函数思想的应用奎屯王新敞新疆授课类型:复习课奎屯王新敞新疆课时安排:1 课时奎屯王新敞新疆教 具:多媒体、实物投影仪奎屯王新敞新疆教学过程: 一、引入:通过上一节学习,大家了解了本章内容的整体结构,明确了本章的重难点知识,并熟悉了有关函数的基本概念和基本方法,这一节,我们将通过例题分析重点掌握数形结合的特征与方法,并进一步认清函数的思想实质,进而掌握其应用.二、例题分析:例 1 若函数 f(x)=x 2 +bx+c 对任意实数 x 都有 f(2+x)=f(2-x),那么( )A.f(2)<f(1)<f(4) B.f(1)<f(2)<f(4)C.f(2)<f(4)<f(1) D.f(4)<f(2)<f(1) 奎屯王新敞新疆分析:此题解决的关键是将函数的对称语言转化为对称轴方程.解:由 f(2+x)=f(2-x)可知:函数 f(x)的对称轴为 x=2,由二次函数 f(x)开口方向向,可得f(2)最小,又 f(4)=f(2+2)=f(2-2)=f(0)在 x<2 时,y=f(x)为减函数 0<1<2,∴f(0)>f(1)>f(2)即 f(2)<f(1)<f(4)奎屯王新敞新疆答案:A奎屯王新敞新疆通过此题可将对称语言推广如下:(1)若对任意实数 x,都有 f(a+x)=f(a-x)成立,则 x=a 是函数 f(x)的对称轴(2)若对任意实数 x,都有 f(a+x)=f(b-x)成立,则 x=2ba 是 f(x)的对称轴.例 2 求 f(x)=x 2 -2ax+2 在[2,4]上的最大值和最小值. 解:先求最小值.因为 f(x)的对称轴是 x=a,可分以下三种情况:(1)当 a<2 时,f(x)在[2,4]上为增函数,所以 f(x)min=f(2)=6-4a;(2)当 2≤a<4 时,f(a)为最小值,f(x)min=2-a 2 ;(3)当 a>4 时,f(x)在[2,4]上为减函数,所以 f(x)min=f(4)=18-8a综上所述:f(x)min=)2( ,818)42( ,2)2( ,462aaaaaa奎屯王新敞新疆最大值为 f(2)与 f(4)中较大者:f(2)-f(4)=(6-4a)-(18-8a)=12+4a(1)当 a≥3 时,f(2)≥f(4),则 f(x)max=f(2)=6-4a; 1 (2)当 a<3 时,f(2)<f(4),则 f(x)max=f(4)=18-8a.故 f(x)max=)3( ,88)3( ,46aaaa评述:本题属于二次函数在给定区间上的最值问题,由于二次函数的系数含有参数,对称轴是变动的,属于“轴动区间定”,由于图象开口向上,所以求最小值要根据对称轴 x=a ...