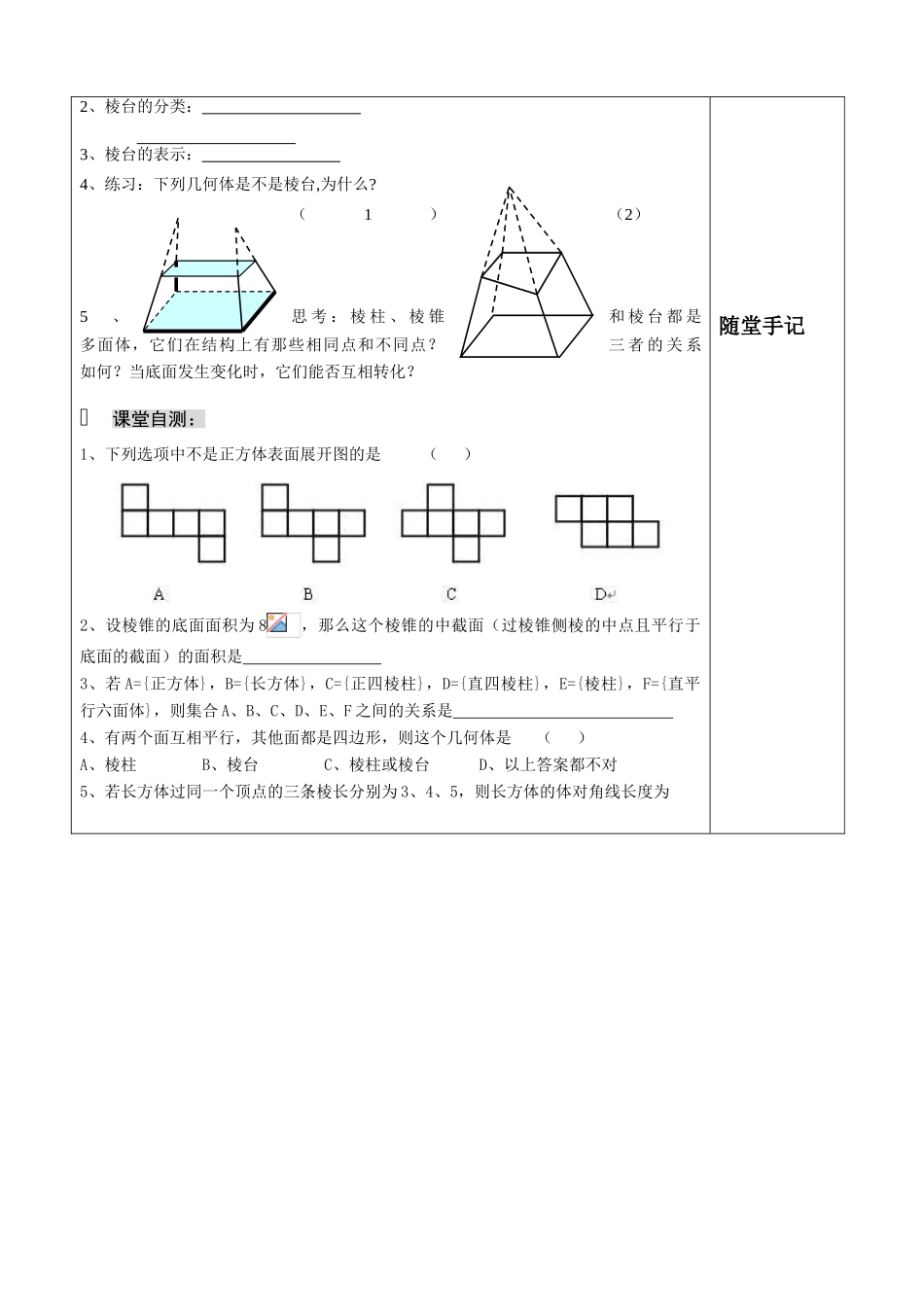
§1.1 空间几何体的结构(一)——多面体学习目标:(1)能根据几何体的结构特征将空间物体进行分类(2)会用语言叙述棱柱、棱锥、棱台的结构特征新课预习:(1)预习课本第 2 页的观察部分,试着将所给出的 16 幅图片进行分类,并说明分类依据。(2)空间几何体的分类: 新课导学(一)棱柱1、 棱柱的结构特征: 2、棱柱的分类: (1)按侧棱与底面垂直与否,分为: 注:底面是正多边形的直棱柱叫做正棱柱。(2)按底面多边形的边数,分为: 3、棱柱的表示: 4、根据右边模型,回答下列问题:(1)观察长方体模型,有多少对平行平面?能作为棱柱底面的有多少对?(2) 如右图,长方体中被截去一部分,其中。问剩下的几何体是什么?截去的几何体是什么(3)观察六棱柱模型,有多少对平行平面?能作为棱柱底面的有多少对?5、补充:平行六面体——底面是平行四边形的四棱柱(二)棱锥1、棱锥的结构特征: 2、棱锥的分类: 注:如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥是正棱锥 . 3、棱锥的表示: (三)棱台1、棱台的结构特征: 随堂手记 对本节课的整体把握: 对棱柱的补充内容: 棱 锥 的 补 充 内容:棱 台 的 补 充 内容: 课后反思:2、棱台的分类: 3、棱台的表示: 4、练习:下列几何体是不是棱台,为什么? (1) (2)5、思 考 : 棱 柱 、 棱 锥和 棱 台 都 是多面体,它们在结构上有那些相同点和不同点?三 者 的 关 系如何?当底面发生变化时,它们能否互相转化?课堂自测:1、下列选项中不是正方体表面展开图的是 ( )2、设棱锥的底面面积为 8,那么这个棱锥的中截面(过棱锥侧棱的中点且平行于底面的截面)的面积是 3、若 A={正方体},B={长方体},C={正四棱柱},D={直四棱柱},E={棱柱},F={直平行六面体},则集合 A、B、C、D、E、F 之间的关系是 4、有两个面互相平行,其他面都是四边形,则这个几何体是 ( )A、棱柱 B、棱台 C、棱柱或棱台 D、以上答案都不对5、若长方体过同一个顶点的三条棱长分别为 3、4、5,则长方体的体对角线长度为 随堂手记6、若长方体的三个面的面积分别为 6、3、2,则长方体的体对角线的长度为 7、若棱锥的所有棱长均相等,则它一定不是 ( ) A、三棱锥 B、四棱锥 C、五棱锥 D、六棱锥8、正四棱锥的高为,侧棱长为,则侧面上斜高的值为 9、棱台不具有的性质是 ( )A、两底面相...