数学数列与不等式的综合问题突破策略VIP免费

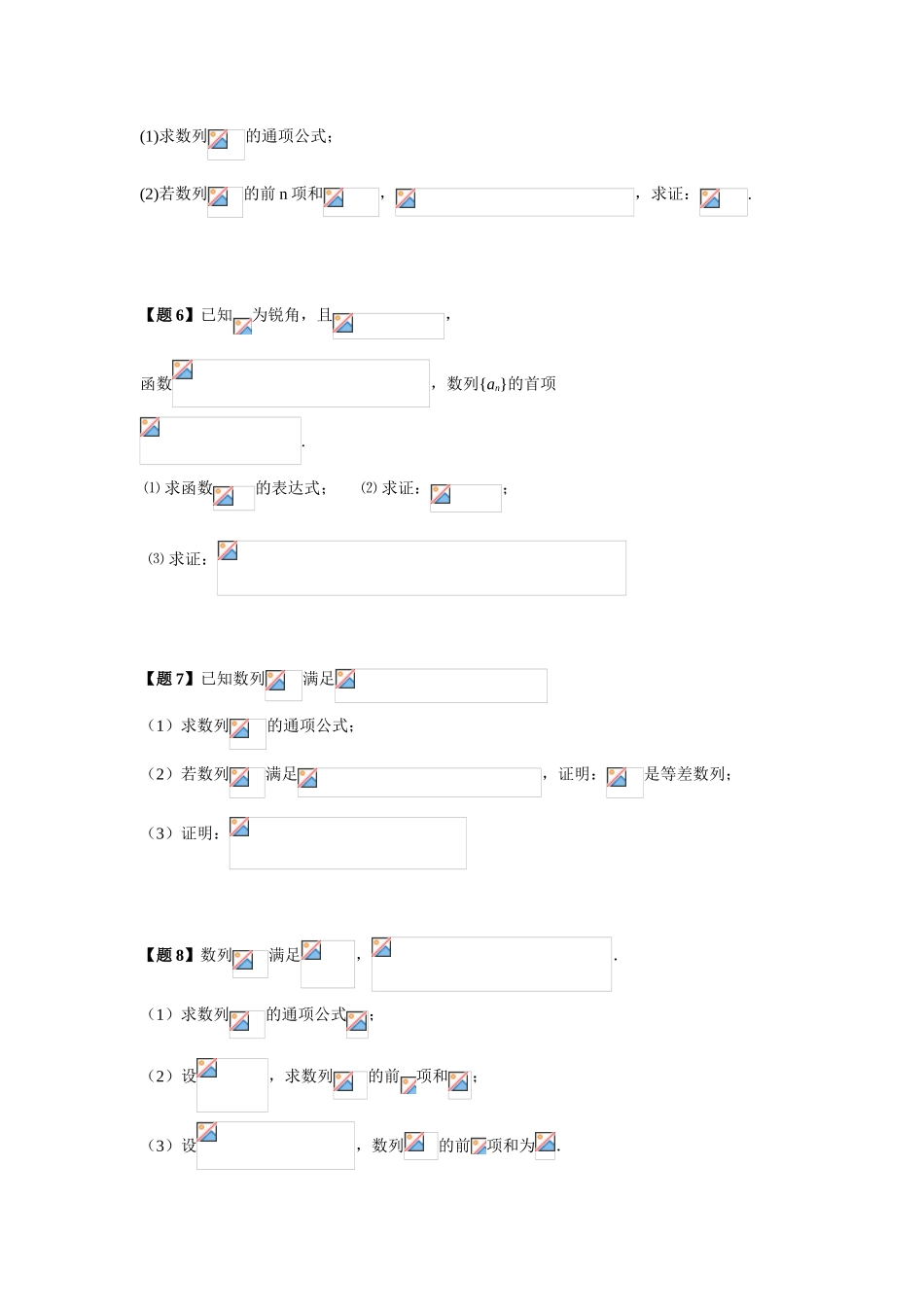
数学数列与不等式的综合问题突破策略【题1】等比数列{an}的公比q＞1，第17项的平方等于第24项，求使a1＋a2＋…＋an＞恒成立的正整数n的范围.【题2】设数列{an}的前项和为Sn．已知a1＝a，an+1＝Sn＋3n，n∈N*．(1)设bn＝Sn－3n，求数列{bn}的通项公式；（2）若an+1≥an，n∈N*，求a的取值范围．【题3】数列{an}是等差数列，其前n项和为Sn，a3＝7，S4＝24．(1)求数列{an}的通项公式；(2)设p、q都是正整数，且p≠q，证明：Sp+q＜(S2p＋S2q)．【题4】已知数列中，（1）设，求证：数列是等比数列；（2）求数列的通项公式（3）设，求证：数列的前项和．【题5】已知数列满足.(1)求数列的通项公式；(2)若数列的前n项和，，求证：.【题6】已知为锐角，且，函数，数列{an}的首项.⑴求函数的表达式；⑵求证：；⑶求证：【题7】已知数列满足（1）求数列的通项公式；（2）若数列满足，证明：是等差数列；（3）证明：【题8】数列满足，．（1）求数列的通项公式；（2）设，求数列的前项和；（3）设，数列的前项和为．求证：对任意的，．【题9】已知数列的前项和为，且对于任意的，恒有，设．（1）求证：数列是等比数列；（2）求数列的通项公式和；（3）若，证明：．【题10】等比数列{an}的首项为a1＝2002，公比q＝－．(1)设f(n)表示该数列的前n项的积，求f(n)的表达式；(2)当n取何值时，f(n)有最大值．【题11】已知{an}的前n项和为Sn，且an＋Sn＝4.(1)求证：数列{an}是等比数列；(2)是否存在正整数k，使＞2成立.【题12】已知数列{an}和{bn}满足：a1＝λ，an+1＝an＋n－4，bn＝(－1)n(an－3n＋21)，其中λ为实数，n为正整数.（1）对任意实数λ，证明数列{an}不是等比数列；（2）试判断数列{bn}是否为等比数列，并证明你的结论；（3）设0＜a＜b,Sn为数列{bn}的前n项和.是否存在实数λ，使得对任意正整数n，都有a＜Sn＜b?若存在，求λ的取值范围；若不存在，说明理由.【题13】设数列满足，且数列是等差数列，数列是等比数列.（1）求数列和的通项公式；（2）是否存在，使，若存在，求出，若不存在，说明理由.数列与不等式综合解答与评析类型1：求有数列参与的不等式恒成立条件下参数问题求数列与不等式相结合恒成立条件下的参数问题主要两种策略：(1)若函数f(x)在定义域为D，则当x∈D时，有f(x)≥M恒成立f(x)min≥M；f(x)≤M恒成立f(x)max≤M；(2)利用等差数列与等比数列等数列知识化简不等式，再通过解不等式解得.【题1】利用条件中两项间的关系，寻求数列首项a1与公比q之间的关系，再利用等比数列前n项公式和及所得的关系化简不等式，进而通过估算求得正整数n的取值范围.【解】由题意得：(a1q16)2＝a1q23，∴a1q9＝1.由等比数列的性质知数列{}是以为首项，以为公比的等比数列，要使不等式成立，则须＞，把a2＝q18代入上式并整理，得q18(qn－1)＞q(1－)，qn＞q19， q＞1，∴n＞19，故所求正整数的取值范围是n≥20.【点评】本题解答数列与不等式两方面的知识都用到了，主要体现为用数列知识化简，用不等式知识求得最后的结果.本题解答体现了转化思想、方程思想及估算思想的应用.【题2】第（1）小题利用Sn与an的关系可求得数列的通项公式；第（Ⅱ）小题将条件an+1≥an转化为关于n与a的关系，再利用a≤f(n)恒成立等价于a≤f(n)min求解．【解】(1)依题意，Sn+1－Sn＝an+1＝Sn＋3n，即Sn+1＝2Sn＋3n，由此得Sn+1－3n+1＝2(Sn－3n)．因此，所求通项公式为bn＝Sn－3n＝(a－3)2n1，n∈N*,①(2)由①知Sn＝3n＋(a－3)2n1，n∈N*，于是，当n≥2时，an＝Sn－Sn1＝3n＋(a－3)2n1－3n1－(a－3)2n2＝2×3n1＋(a－3)2n2，an+1－an＝4×3n1＋(a－3)2n2＝2n2·[12·()n2＋a－3]，当n≥2时，an+1≥an，即2n2·[12·()n2＋a－3]≥0，12·()n2＋a－3≥0，∴a≥－9，综上，所求的a的取值范围是[－9，＋∞)【点评】一般地，如果求条件与前n项和相关的数列的通项公式，则可考虑Sn与an的关系求解.本题求参数取值范围的方法也一种常用的方法，应当引起重视.类型2：数列参与的不等式的证明问题此类不等式的证明常用的方法：(1)比较法，特别是差值比较法是最根本的方法；(2)分析法与综合法...