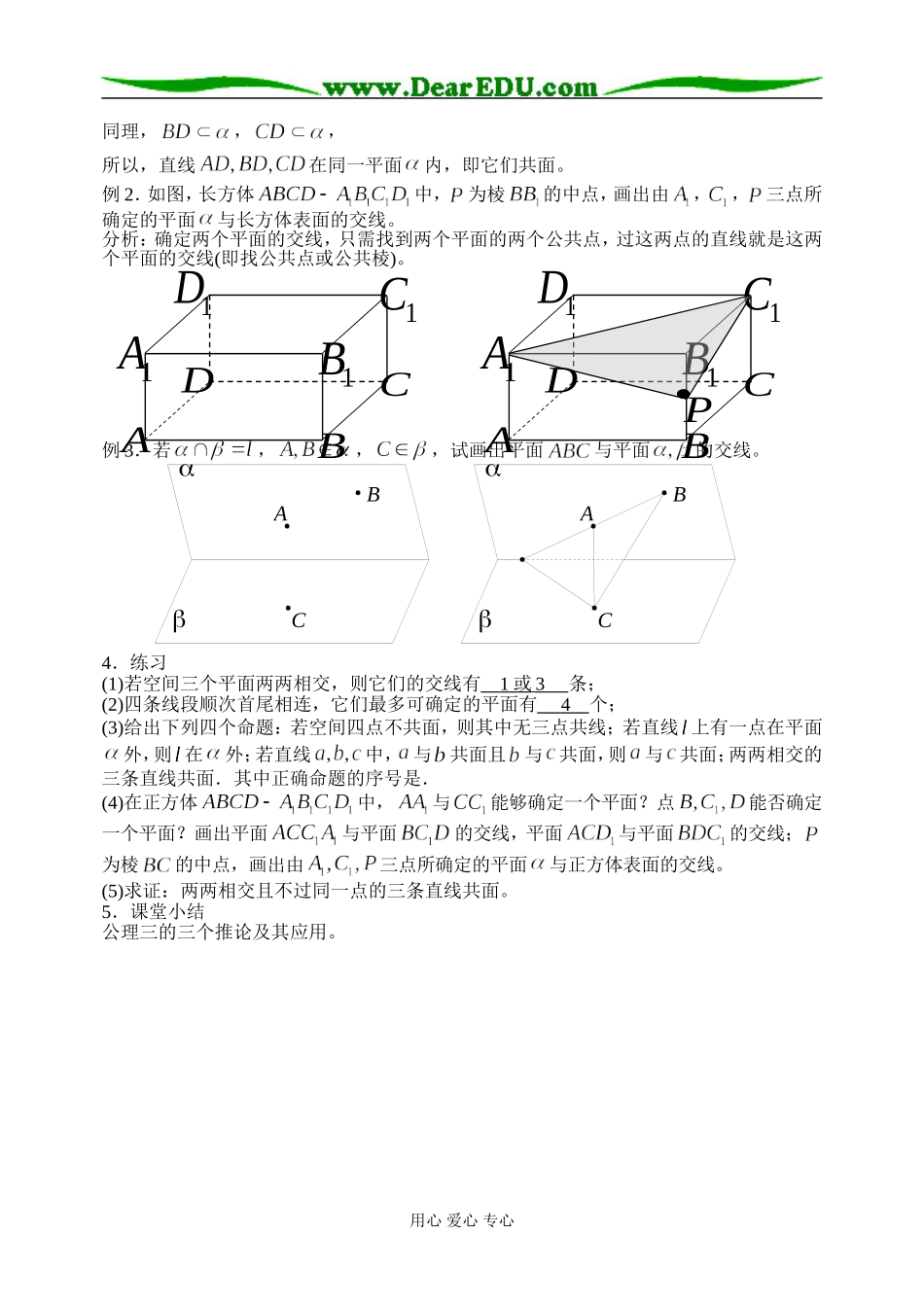
§1.2.1 平面的基本性质(2)教学目标:1.了解推论 1、推论 2、推论 3,并能运用推论解释生活中的一些现象.2.初步学习立体几何中的证明.教学重点:三个推论的理解和应用.教学难点:推论的正确理解和正确应用.教学过程:1.复习引入复习:回顾平面的基本性质的三个公理:公理 1、公理 2、公理 3.问题:根据公理 3,不共线的三个点可以确定一个平面,那么,一条直线和这条直线外一点能否确定一个平面呢?两条相交直线呢?两条平行直线呢?为什么?2.公理 3 的三个推论推论 1:经过一条直线和直线外的一点有且只有一个平面.已知:直线 ,点,求证:过点和直线 有且只有一个平面。证明:(存在性):在直线 上任取两点、, ,∴不共线.由公理 3,经过不共线的三点可确定一个平面, 点,根据公理 1,∴,即平面经过直线 和点。(唯一性): ,∴经过直线 和点的平面一定经过点,又 由公理 3 可得:经过不共线三点的平面只有一个,所以,经过 和点的平面只有一个。类似地,得出以下两个推论:(由学生证明)推论 2:经过两条相交直线有且只有一个平面。证明:(存在性):设,在上取不同于点的点,则,由推论 1 得,过直线和点有一个平面,,,因此,经过有一个平面。(唯一性):经过的平面一定经过和,由推论 1,这样的平面只有一个,所以经过两条相交直线的平面有且只有一个。推论 3:经过两条平行直线有且只有一个平面。3.例题讲解例 1.已知:,求证:直线共面。分析: 直线 与点可以确定平面,∴只需证明都在平面内。证明: ,∴直线 与点可以确定平面(推论 1),又 ,∴,又 ,∴(公理 1),用心 爱心 专心A BCD l同理,,,所以,直线在同一平面内,即它们共面。例 2.如图,长方体中,为棱的中点,画出由,,三点所确定的平面与长方体表面的交线。分析:确定两个平面的交线,只需找到两个平面的两个公共点,过这两点的直线就是这两个平面的交线(即找公共点或公共棱)。例 3.若,,,试画出平面与平面的交线。4.练习(1)若空间三个平面两两相交,则它们的交线有 1 或 3 条;(2)四条线段顺次首尾相连,它们最多可确定的平面有 4 个;(3)给出下列四个命题:若空间四点不共面,则其中无三点共线;若直线 上有一点在平面外,则 在外;若直线中, 与共面且与共面,则与共面;两两相交的三条直线共面.其中正确命题的序号是.(4)在正方体中,与能够确定一个平面?点能否确定一个平面?画出平面...