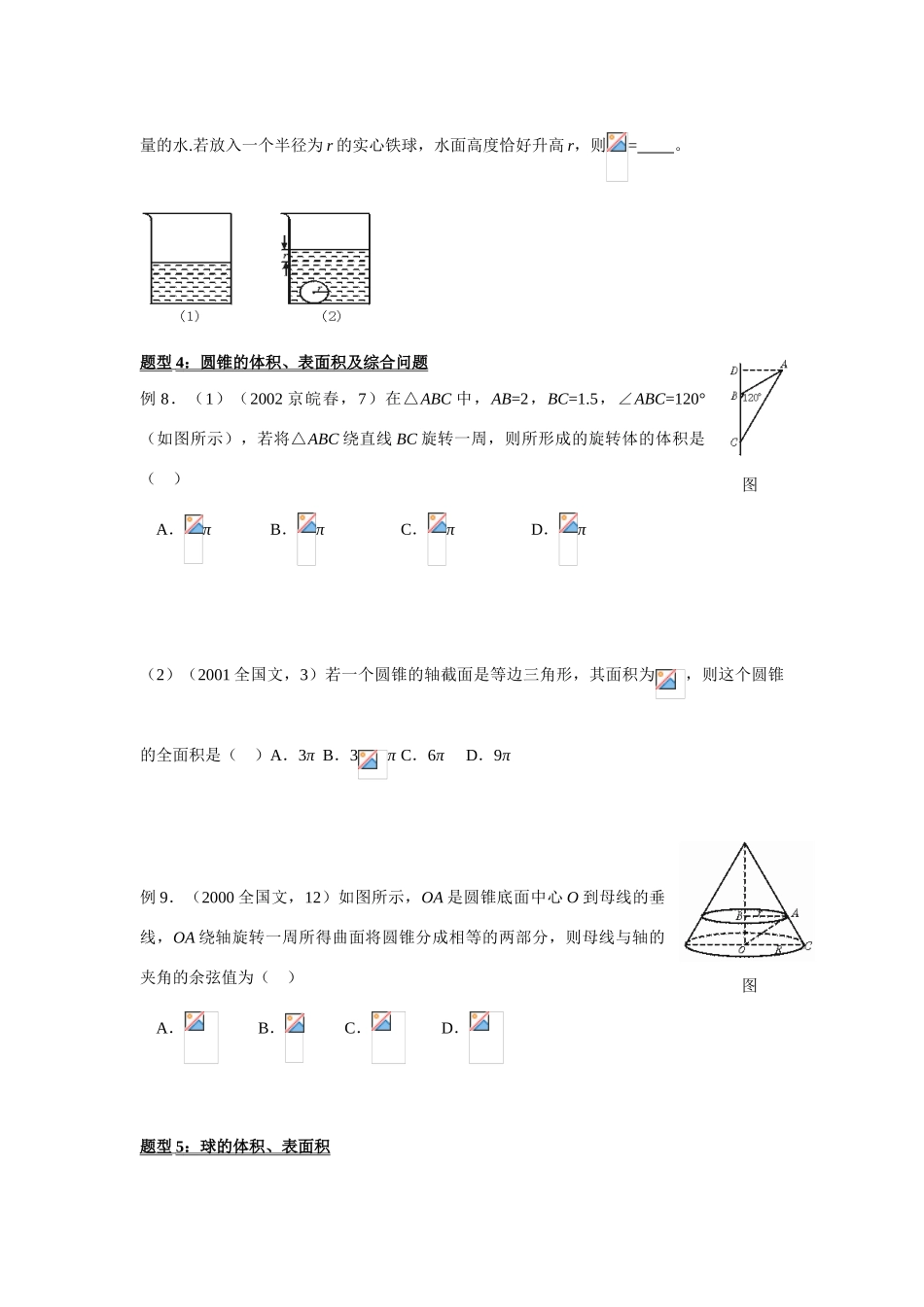
PABCDO41 中高三数学第一轮复习—空间几何体的表面积和体积一.命题走向由于本讲公式多反映在考题上,预测 008 年高考有以下特色:(1)用选择、填空题考查本章的基本性质和求积公式;(2)考题可能为:与多面体和旋转体的面积、体积有关的计算问题;与多面体和旋转体中某些元素有关的计算问题;二.要点精讲1.多面体的面积和体积公式名称侧面积(S 侧)全面积(S 全)体 积(V)棱柱棱柱直截面周长×lS 侧+2S 底S 底·h=S 直截面·h直棱柱chS 底·h棱锥棱锥各侧面积之和S 侧+S 底S 底·h正棱锥ch′棱台棱台各侧面面积之和S 侧+S 上底+S 下底h(S 上底+S 下底+)正棱台 (c+c′)h′表中 S 表示面积,c′、c 分别表示上、下底面周长,h 表斜高,h′表示斜高,l 表示侧棱长。2.旋转体的面积和体积公式名称圆柱圆锥圆台球S 侧2πrlπrlπ(r1+r2)lS 全2πr(l+r)πr(l+r)π(r1+r2)l+π(r21+r22)4πR2Vπr2h(即πr2l)πr2hπh(r21+r1r2+r22)πR3表中 l、h 分别表示母线、高,r 表示圆柱、圆锥与球冠的底半径,r1、r2分别表示圆台 上、下底面半径,R 表示半径。四.典例解析题型 1 :柱体的体积和表面积 例 1.一个长方体全面积是 20cm2,所有棱长的和是 24cm,求长方体的对角线长.例 2.如图,三棱柱 ABC—A1B1C1中,若 E、F 分别为 AB、AC 的中点,平面 EB1C1 将 三 棱 柱 分 成 体 积 为 V1 、 V2 的 两 部 分 , 那 么 V1∶V2= ____ _。题型 2 :锥体的体积和表面积 例 3.(2006 上海,19)在四棱锥 P-ABCD 中,底面是边长为 2 的菱形,∠DAB=60 ,对角线 AC 与 BD 相交于点 O,PO⊥平面 ABCD,PB与平面 ABCD 所成的角为 60 ,求四棱锥 P-ABCD 的体积?例 4.(2006 江西理,12)如图,在四面体 ABCD 中,截面 AEF经过四面体的内切球(与四个面都相切的球)球心 O,且与BC,DC 分别截于 E、F,如果截面将四面体分成体积相等的两部分,设四棱锥 A-BEFD 与三棱锥 A-EFC 的表面积分别是S1,S2,则必有( )A.S1S2 B.S1S2C.S1=S2 D.S1,S2的大小关系不能确定题型 3 :棱台的体积、面积 例 5.(1)(1998 全国,9)如果棱台的两底面积分别是 S、S′,中截面的面积是 S0,那么( )A. B. C.2S0=S+S′ D.S02=2S′S(2)(1994 全国,7)已知正六棱台的上、下底面边长分别为 2 和 4,高为 2,则其体积为( )A.32...