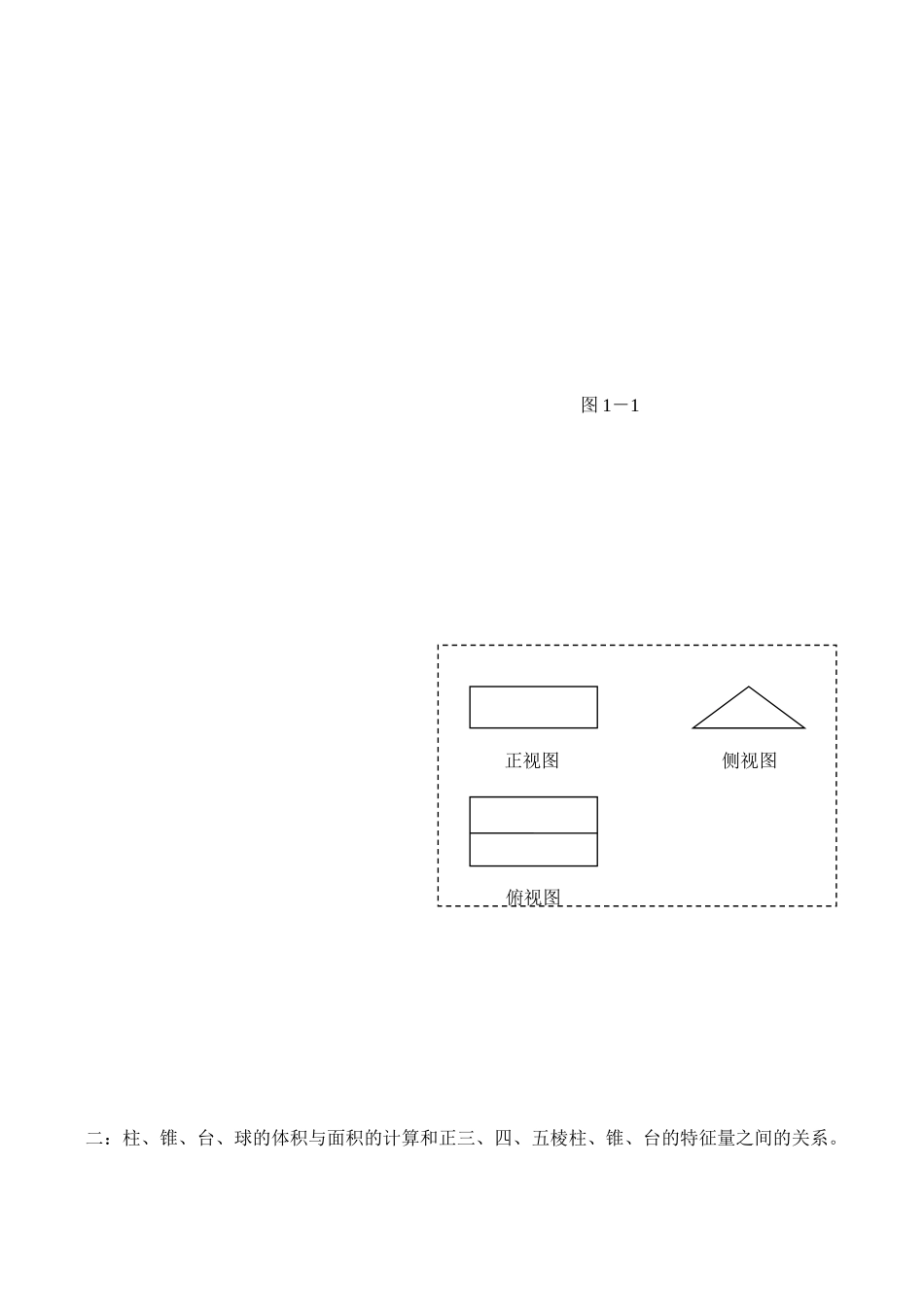
2008 高考数学复习 空间几何体学案一、三视图的关系与画法;斜二侧直观图;例 1 如图 1-1 是一个几何体的三视图(单位:cm)(Ⅰ)画出这个几何体的直观图(不要求写画法);(Ⅱ)求这个几何体的表面积及体积;(Ⅲ)设异面直线与所成的角为,求.二:柱、锥、台、球的体积与面积的计算和正三、四、五棱柱、锥、台的特征量之间的关系。俯视图正视图侧视图图 1-1例2.(2007广东·文) 已知某几何体的俯视图是如图5所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形. (1)求该几何体的体积V; (2)求该几何体的侧面积S例 3.如图,在三棱锥 A—BC D 中,BD=,AB=BC=CD=DA= AC=,E、F、G、H 分别是 AB、BC、CD、DA 的中点. (Ⅰ)求证:四边形 EFGH 是矩形;(Ⅱ)求证:平面 ABD平面DCB. 例 4 . 如 图 , 在 直 四 棱 柱中 , 已 知,.(1)求证:;(2)设是上一点,试确定的位置,使平面,并说明理由.BCDA俯视图主视图左视图第 4 题图【考点小测】 1.下列几何体各自的三视图中,有且仅有两个视图相同的是( )A.①②B.①③C.①④D.②④2.如图,正三棱柱的各棱长都 2,E,F 分别是的中点,则 EF 的长是 3.棱长为 3 的正方体的顶点都在同一球面上,则该球的表面积为______.4.如图(下面),一个简单空间几何体的三视图其主视图与左视图是边长为 2 的正三角形、俯视图轮廓为正方形,则其体积是 . 5. 若一个正三棱柱的三视图如下图所示,则这个正三棱柱的高和底面边长分别为( ) (A)2,2 (B) 2,2 (C)4,2 (D)2,46. 平面几何的很多性质可以推广到空间,如“两条对角线相等的平行四边形是矩形”推广到空间是“对角线相等的平行六面体是长方① 正方形② 圆锥③ 三棱台④ 正四棱锥主视图俯视图2 左视图左视图主视图俯视图第 7 题体”,请你把性质“平行四边形的两条对角线的平方和等于四边的平方和”推广到空间的命题是“ ”7.如图,一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为 1,那么这个几何体的体积为 . 8. 如图,在四棱锥中,底面,,,是的中点.(1)证明;(2)证明平面;9.四面体的一条棱长是 x,其他各条棱长为 1.(1)把四面体的体积 V 表示为x 的函数 f(x);(2)求 f(x)的值域;(3)求 f(x)的单调区间.[附加...