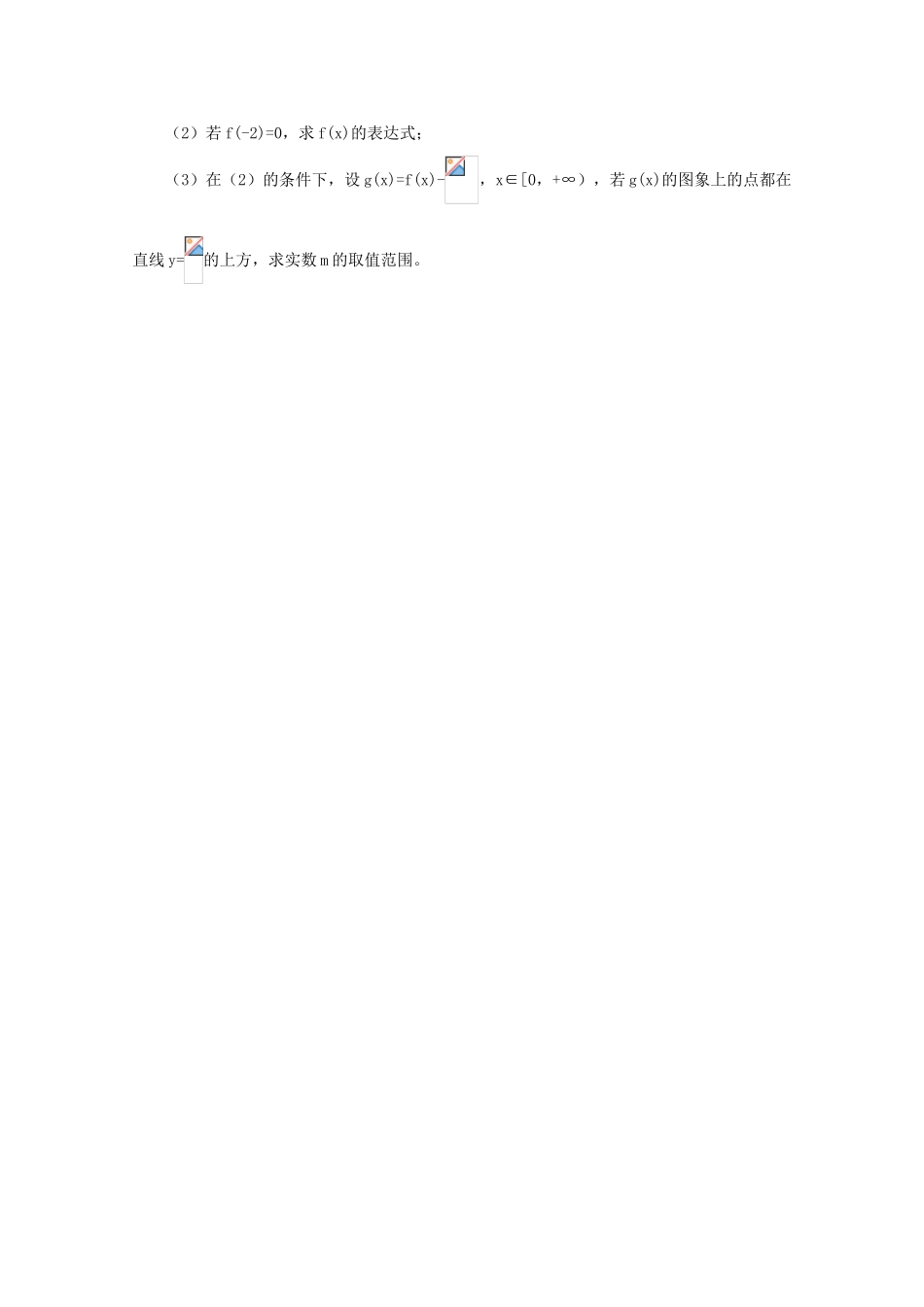
第 48 课时 函数综合(一) 1、函数 y=x-在(1,+∞)上是增函数,则实数 p 的取值范围为_________2、在等差数列{an}中,,若它的前 n 项和 Sn 有最大值,那么{Sn}中的最小正数是__________3、已知 x>0,y=x+的最小值为__________4、f(x)=x3+3x,若 f(msinθ)+f(1-m)>0()恒成立,则实数 m 的取值范围为___________5 、 定 义 在 ( 0 , +∞ ) 上 的 函 数 f(x) 的 导 函 数 f'(x)<0 恒 成 立 , 且 f(4)=1 , 若f(x+y)≤1,则 x2+y2+2x+2y 的最小值为__________6、设 P 是椭圆上任意一点,A 和 F 分别是椭圆的左顶点和右焦点,则的最小值为________7 、 已 知 A 、 B 、 C 是 直 线 l 上 不 同 的 三 点 , O 是 任 意 一 点 , 且 满 足,若对a∈[-1,1],都有 af(x)-4x≥0 恒成立,则实数x 的取值范围为__________8、设函数 f(x)=lnx(1)证明函数 g(x)=f(x)-在 x∈(1,+∞)上是单调增函数。(2)若不等式 1-x2≤f(e1-2x)+m2-2bm-2,当 b∈[-1,1]时恒成立,求实数 m 的取值范围。9、设函数 f(x)=sinx+cosx 和 g(x)=2sinxcosx(1)若 a 为实数,试求 F(x)=f(x)+ag(x),x∈[0,]的最小值 h(a)。(2)若存在 x∈[0,],使|af(x)-g(x)-3|≥成立,求实数 a 的取值范围。10、已知二次函数 f(x)=ax2+bx+c,满足对任意实数 x 都有 f(x)≥x,且当 x∈(1,3)时,f(x)成立。(1)证明 f(2)=2;(2)若 f(-2)=0,求 f(x)的表达式;(3)在(2)的条件下,设 g(x)=f(x)-,x∈[0,+∞),若 g(x)的图象上的点都在直线 y=的上方,求实数 m 的取值范围。