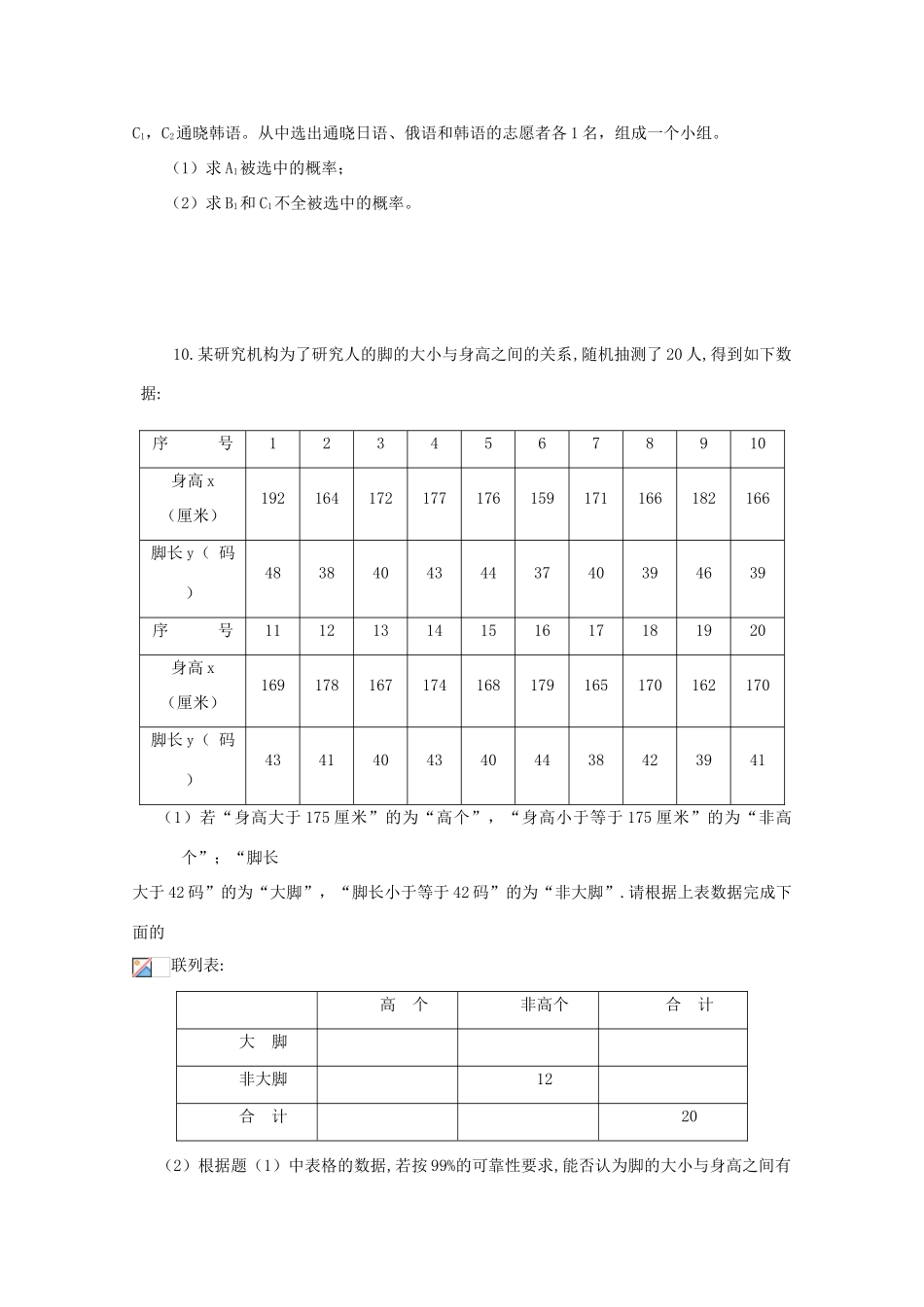
第 47 讲 专题训练九概率统计应用题1.已知圆的方程为 x2+y2-6x-8y=0 设该圆过点(3,5)的最短弦和最长弦分别为 AC 和BD,则四边形 ABCD 面积为 2.已知 Z∈C 且=1 则的最小值为___________ 3.已知实数 a、b 满足-1≤a≤1,-1≤b≤1 则方程 x2-2ax+b2=0 有实数解的概率为________4.若点 p 是曲线 y=x2-lnx 上任意一点,则点 p 到直线 y=x-2 的最小距离为________5.已知 a2008与 a2009是首项为正数的等差数列{an}的相邻两项,且函数 y=(x-a2008)(x-a2009)图象与 x 轴的两个交点横坐标分别在区间(-3,-2)和(0,1)上,则使前 n 项和 Sn 取得最大值的自然数 n 是_________,使前 n 项和 Sn>0 成立的最大自然数 n 是__________6.若 r(x):sinx+cosx>m,S(x):x2+mx+1>0,如果对于任意 x∈R,r(x)为假命题,s(x)为真命题,则 m 的范围是___________7.在轴截面是边长为 2 的正方形 ABCD 的无盖圆柱桶上动点 P 从母线 AB 的端点 A(A 在桶底),从桶外运动到桶内母线 CD 的中点 M 的最短路线长为__________8.为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6 名学生进行问卷调查,6 人得分情况如下:5,6,7,8,9,10。把这 6 名学生的得分看成一个总体。(1)求该总体的平均数;(2)用简单随机抽样方法从这 6 名学生中抽取 2 名,他们的得分组成一个样本。求该样本平均数与总体平均数之差的绝对值不超过 0.5 的概率。9.现有 8 名奥运会志愿者,其中志愿者 A1,A2,A3 通晓日语,B1,B2,B3 通晓俄语C1,C2通晓韩语。从中选出通晓日语、俄语和韩语的志愿者各 1 名,组成一个小组。(1)求 A1被选中的概率;(2)求 B1和 C1不全被选中的概率。10.某研究机构为了研究人的脚的大小与身高之间的关系,随机抽测了 20 人,得到如下数据:序 号12345678910身高 x(厘米)192164172177176159171166182166脚长 y( 码 )48384043443740394639序 号11121314151617181920身高 x(厘米)169178167174168179165170162170脚长 y( 码 )43414043404438423941(1)若“身高大于 175 厘米”的为“高个”,“身高小于等于 175 厘米”的为“非高个”;“脚长大于 42 码”的为“大脚”,“脚长小于等于 42 码”的为“非大脚”.请根据上表数据完成下面的联列表: 高 个非高个合 计大 脚非大脚12合 计20 (2)根据题(1)中表格的数据,若按 99%的可靠性要求,能否认为脚的大小与身高之间有关系? (3)若按下面的方法从这 20 人中抽取 1 人来核查测量数据的误差:将一个标有数字1,2,3,4,5,6 的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号.试求:① 抽到 12 号的概率;②抽到“无效序号(超过 20 号)”的概率.