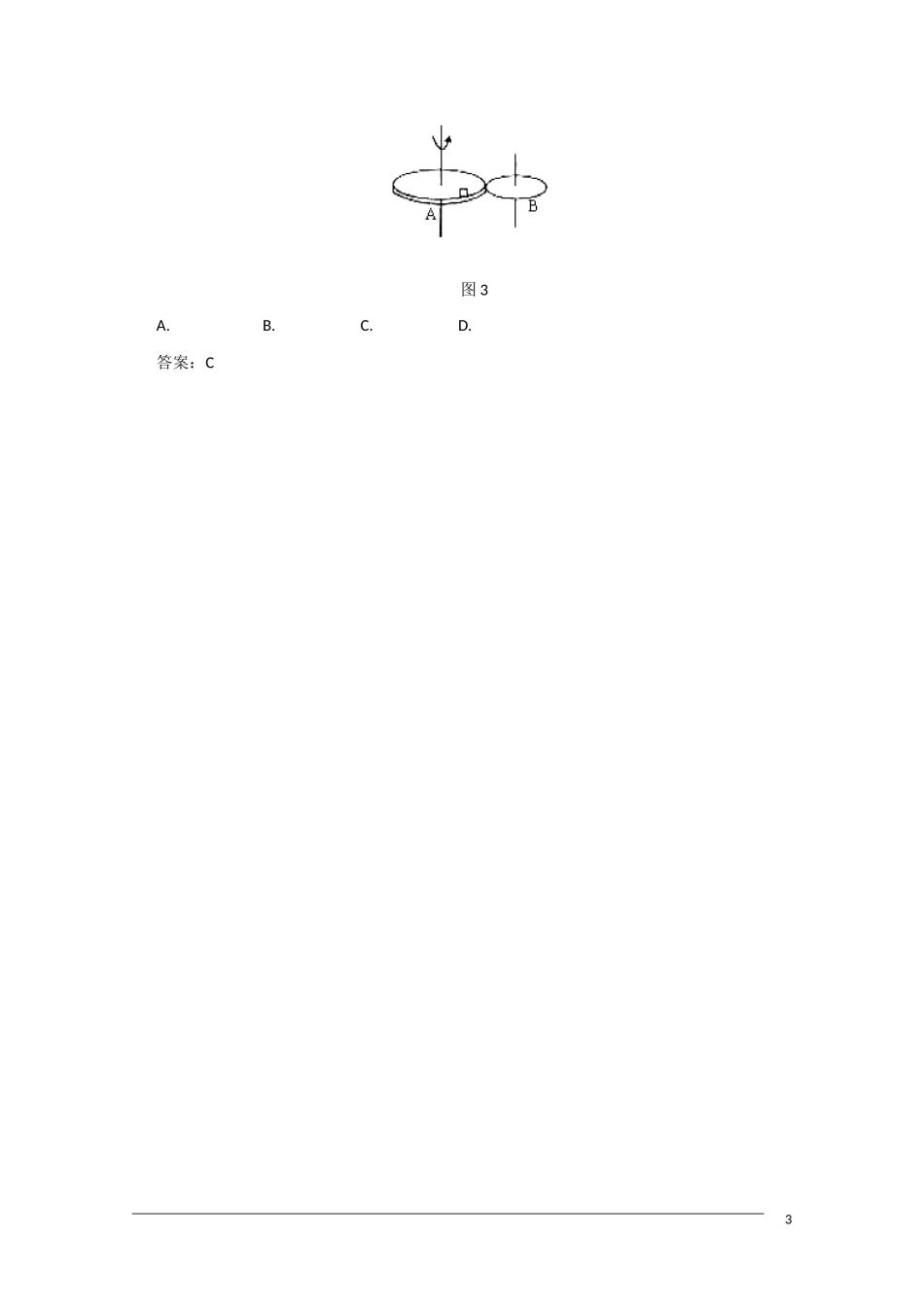
模型组合讲解——水平方向的圆盘模型[模型概述]水平方向上的“圆盘”模型大多围绕着物体与圆盘间的最大静摩擦力为中心展开的,因此最大静摩擦力的判断对物体临界状态起着关键性的作用。[模型讲解]例 1. 如图 1 所示,水平转盘上放有质量为 m 的物块,当物块到转轴的距离为 r 时,连接物块和转轴的绳刚好被拉直(绳上张力为零)。物体和转盘间最大静摩擦力是其正压力的 μ 倍,求:图 1(1)当转盘的角速度 时,细绳的拉力 。(2)当转盘的角速度 时,细绳的拉力 。解析:设转动过程中物体与盘间恰好达到最大静摩擦力时转动的角速度为 ,则 ,解得 。(1)因为 ,所以物体所需向心力小于物体与盘间的最大摩擦力,则物与盘间还未到最大静摩擦力,细绳的拉力仍为 0,即 。(2)因为 ,所以物体所需向心力大于物与盘间的最大静摩擦力,则细绳将对物体施加拉力 ,由牛顿的第二定律得: ,解得 。例 2. 如图 2 所示,在匀速转动的圆盘上,沿直径方向上放置以细线相连的 A、B 两个小物块 。A 的质量为 ,离轴心 ,B 的质量为 ,离轴心 ,A、B 与盘面间相互作用的摩擦力最大值为其重力的 0.5 倍,试求1图 2(1)当圆盘转动的角速度 为多少时,细线上开始出现张力?(2)欲使 A、B 与盘面间不发生相对滑动,则圆盘转动的最大角速度为多大?( )解析:(1) 较小时,A、B 均由静摩擦力充当向心力, 增大, 可知,它们受到的静摩擦力也增大,而 ,所以 A 受到的静摩擦力先达到最大值。 再增大,AB 间绳子开始受到拉力。由 ,得: (2) 达到 后, 再增加,B 增大的向心力靠增加拉力及摩擦力共同来提供,A 增大的向心力靠增加拉力来提供,由于 A 增大的向心力超过 B 增加的向心力, 再增加,B 所受摩擦力逐渐减小,直到为零,如 再增加,B 所受的摩擦力就反向,直到达最大静摩擦力。如 再增加,就不能维持匀速圆周运动了,A、B 就在圆盘上滑动起来。设此时角速度为 ,绳中张力为 ,对 A、B 受力分析:对 A 有 对 B 有 联立解得: [模型要点]水平方向上的圆盘转动时,物体与圆盘间分为有绳与无绳两种,对无绳情况向心力是由“圆盘”对物体的静摩擦力提供,对有绳情况考虑向心力时要注意临界问题。若 ,物体做圆周运动,有绳与无绳一样;若 ,无绳物体将向远离圆心的方向运动;有绳拉力将起作用。[模型演练]如图 3 所示,两个相同材料制成的靠摩擦传动的轮 A...