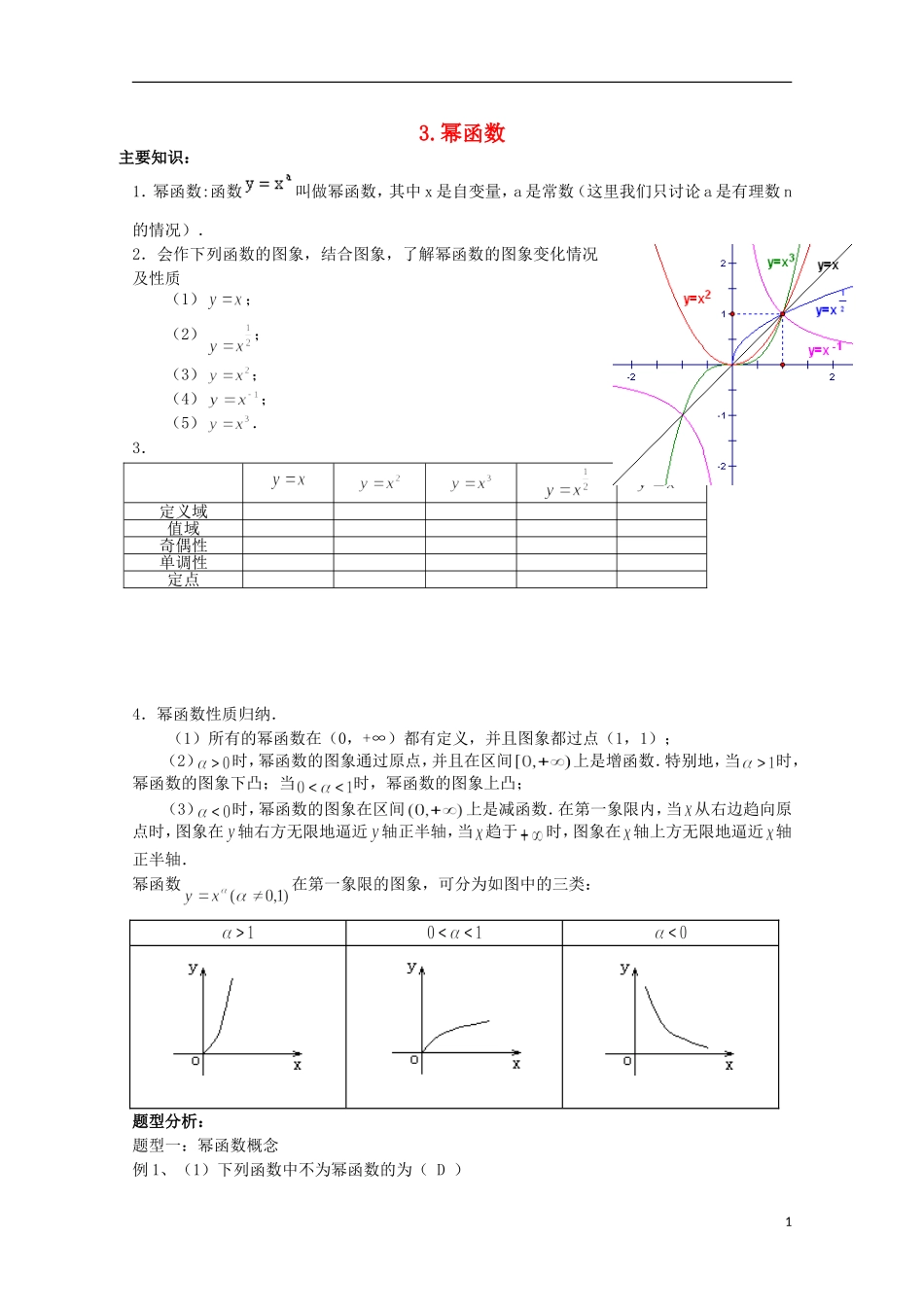
3.幂函数主要知识:1.幂函数:函数叫做幂函数,其中 x 是自变量,a 是常数(这里我们只讨论 a 是有理数 n的情况).2.会作下列函数的图象,结合图象,了解幂函数的图象变化情况及性质(1);(2);(3);(4);(5). 3.4.幂函数性质归纳.(1)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1);(2)时,幂函数的图象通过原点,并且在区间上是增函数.特别地,当时,幂函数的图象下凸;当时,幂函数的图象上凸;(3)时,幂函数的图象在区间上是减函数.在第一象限内,当 从右边趋向原点时,图象在轴右方无限地逼近轴正半轴,当 趋于时,图象在 轴上方无限地逼近 轴正半轴.幂函数在第一象限的图象,可分为如图中的三类:题型分析:题型一:幂函数概念例 1、(1)下列函数中不为幂函数的为( D )定义域值域奇偶性单调性定点1A. B. C. D. (2)下列命题中,正确命题的序号是 ④ ① 当时函数的图象是一条直线;② 幂函数的图象都经过(0,0)和(1,1)点;③ 若幂函数是奇函数,则是定义域上的增函数;④ 幂函数的图象不可能出现在第四象限.例 2(1)函数的定义域是(B )A.{x|x≠0 或 x≠2}B.(-∞,0) (2,+∞)C.(-∞,0) [2,+∞ )D.(0,2)(2)已知幂函数的图象不过原点,则 m 的值为_________。3题型二:幂函数图象性质例 3(1)当 x∈(1,+∞)时,函数axy 的图象恒在 y=x 的下方,则 a 的取值范围是_________。a<1(2)右图为幂函数在第一象限的图象,则按由小到大的顺序排列为例 4 幂函数,当取不同的正数时,在区间上它们的图象是一族美丽的曲线(如图),设点,连结,线段恰好被其中的两个幂函数的图象三等分,即有。那么 。题型三:比较大小例 5.(1)若,比较的大小;(2)若,比较的大小.解:(1)当时,幂函数在上单调减, ,∴.(2)当时,,指数函数在上单调减, ,∴,∴ , ∴ 题型四:幂函数的综合应用例 6.已知幂函数的图象与轴、 轴都无交点,且关于轴对称,试确定 f x( ) 的解析式.解:由数,解得:.当和 3 时,;当时,.2备用: 已知函数(1)求函数的定义域、值域;(2)判断函数的奇偶性;(3)求函数的单调区间.解:这是复合函数问题,利用换元法令 t=15-2x-x2,则 y=,(1)由 15-2x-x2≥0 得函数的定义域为[-5,3],∴t=16-(x-1)2[0,16].∴函数的值域为[0,2].(2) 函数...