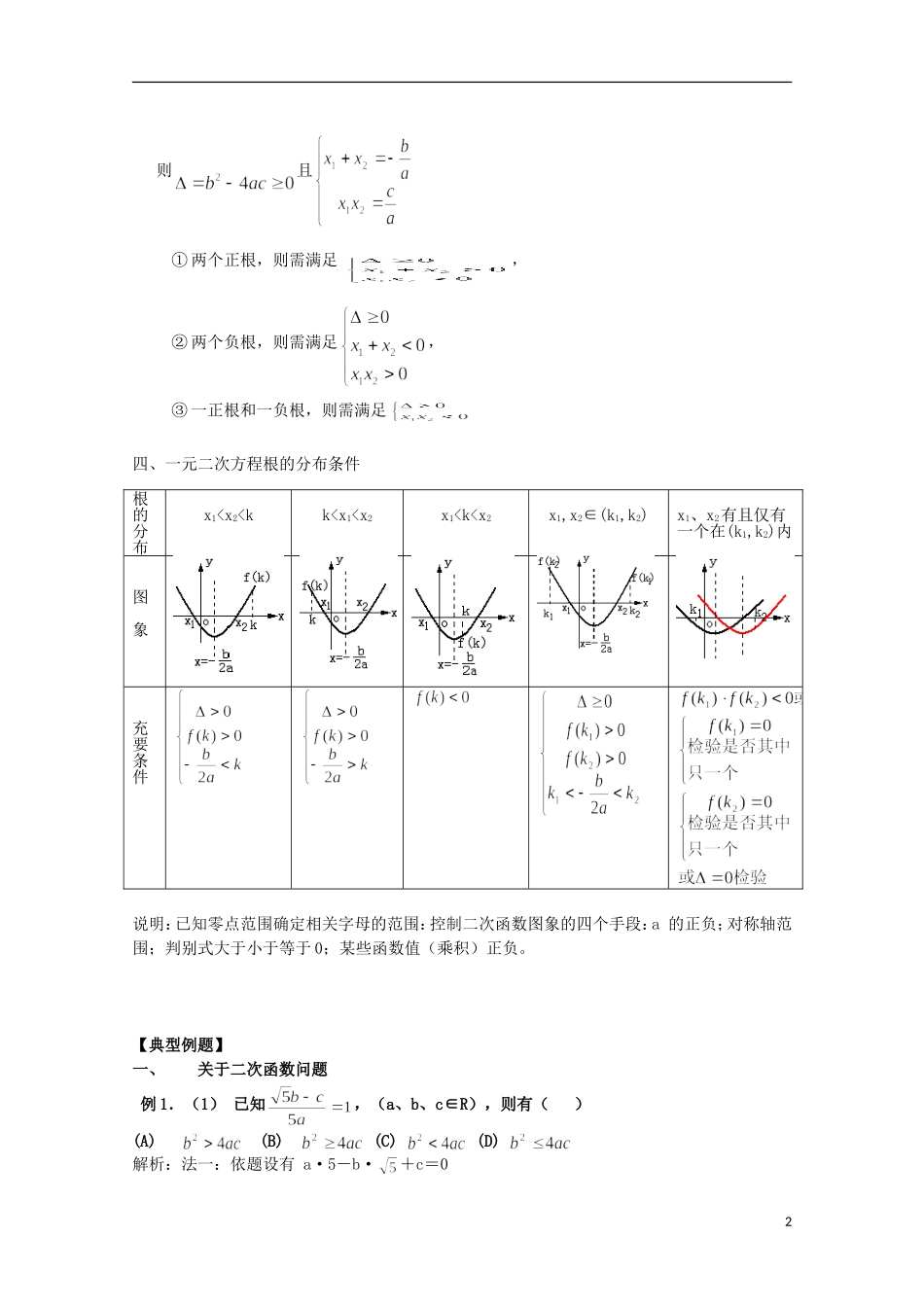
1.函数与方程(1)【知识归纳】一、二次函数的图象和性质1.二次函数的解析式的三种形式(1)一般式:f(x)=ax2+bx+c(a≠0)(2)顶点式(配方式):f(x)=a(x-h)2+k 其中(h,k)是抛物线的顶点坐标。(3)两根式(因式分解):f(x)=a(x-x1)(x-x2),其中 x1,x2是抛物线与 x 轴两交点的坐标。2 . 二 次 函 数 f(x)=ax2+bx+c(a≠0) 的 图 象 是 一 条 抛 物 线 , 对 称 轴, 顶 点 坐 标(1)a>0 时,抛物线开口向上,函数在上单调递减,在上单调递增,时,(2)a<0 时,抛物线开口向下,函数在上单调递增,在上单调递减,时,3 . 二 次 函 数 f(x)=ax2+bx+c(a≠0) 当时 图 象 与 x 轴 有 两 个 交 点M1(x1,0),M2(x2,0),二、三个二次(二次函数、一元二次方程及一元二次不等式)的关系设 a>0,x1x2是方程 ax2+bx+c=0 的两个实根, △情况类型△>0△=0△<0图象ax2+bx+c=0 的 解即函数零点x=x1或 x=x2(x10 解xx2x≠x1 Rax2+bx+c<0 解x10 恒成立问题含参不等式 ax +bx+c>0 的解集是 R;其解答分 a=0(验证 bx+c>0 是否恒成立)、a≠0(a<0 且△<0)两种情况三、实系数一元二次方程 的实根符号与系数的关系:韦达定理:方程()的二实根为、,1则且① 两个正根,则需满足,② 两个负根,则需满足,③ 一正根和一负根,则需满足 四、一元二次方程根的分布条件说明:已知零点范围确定相关字母的范围:控制二次函数图象的四个手段:a 的正负;对称轴范围;判别式大于小于等于 0;某些函数值(乘积)正负。【典型例题】一、关于二次函数问题 例 1.(1) 已知,(a、b、c∈R),则有( )(A) (B) (C) (D) 解析:法一:依题设有 a·5-b·+c=0根的分布x1