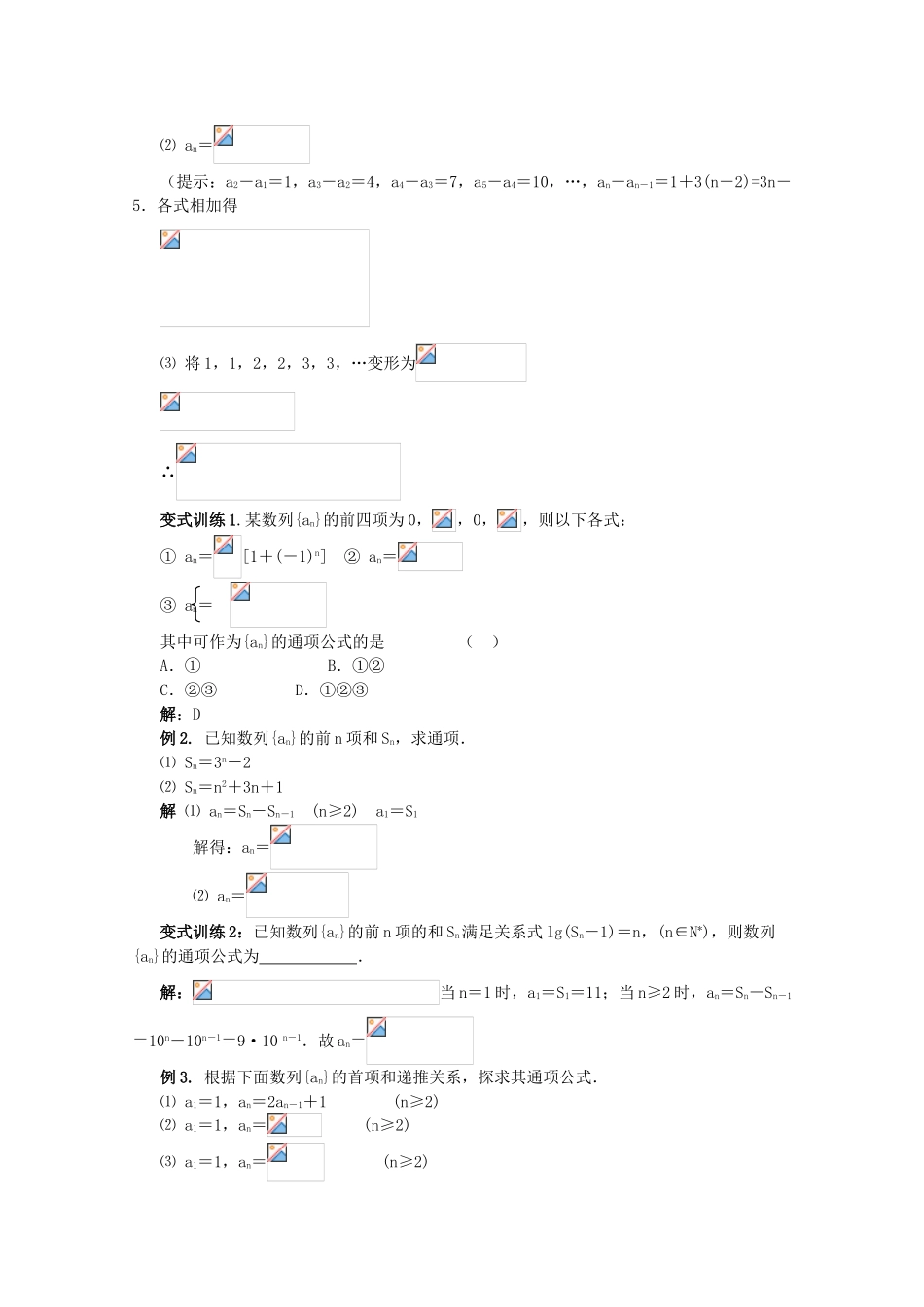
数列1、理解数列的概念,了解数列通项公式的意义.了解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前几项.2、理解等差数列的概念,掌握等差数列的通项公式与前 n 项和的公式,并能解决简单的实际问题.3、理解等比数列的概念,掌握等比数列的通项公式与前 n 项和公式,并能解决简单的实际问题. 纵观近几年高考试题,对数列的考查已从最低谷走出,估计以后几年对数列的考查的比重仍不会减小,等差、等比数列的概念、性质、通项公式、前 n 项和公式的应用是必考内容,数列与函数、三角、解析几何、组合数的综合应用问题是命题热点.从解题思想方法的规律着眼,主要有:① 方程思想的应用,利用公式列方程(组),例如等差、等比数列中的“知三求二”问题;② 函数思想方法的应用、图像、单调性、最值等问题;③ 待定系数法、分类讨论等方法的应用.第 1 课时 数列的概念1.数列的概念:数列是按一定的顺序排列的一列数,在函数意义下,数列是定义域为正整数 N*或其子集{1,2,3,……n}的函数 f(n).数列的一般形式为 a1,a2,…,an…,简记为{an},其中 an是数列{an}的第 项.2.数列的通项公式一个数列{an}的 与 之间的函数关系,如果可用一个公式 an=f(n)来表示,我们就把这个公式叫做这个数列的通项公式.3.在数列{an}中,前 n 项和 Sn与通项 an的关系为: 4.求数列的通项公式的其它方法⑴ 公式法:等差数列与等比数列采用首项与公差(公比)确定的方法.⑵ 观察归纳法:先观察哪些因素随项数 n 的变化而变化,哪些因素不变;初步归纳出公式,再取 n 的特珠值进行检验,最后用数学归纳法对归纳出的结果加以证明.⑶ 递推关系法:先观察数列相邻项间的递推关系,将它们一般化,得到的数列普遍的递推关系,再通过代数方法由递推关系求出通项公式.例 1. 根据下面各数列的前 n 项的值,写出数列的一个通项公式.⑴ -,,-,…;⑵ 1,2,6,13,23,36,…;⑶ 1,1,2,2,3,3,解: ⑴ an=(-1)n典型例题基础过关知识网络考纲导读高考导航⑵ an=(提示:a2-a1=1,a3-a2=4,a4-a3=7,a5-a4=10,…,an-an-1=1+3(n-2)=3n-5.各式相加得⑶ 将 1,1,2,2,3,3,…变形为∴变式训练 1.某数列{an}的前四项为 0,,0,,则以下各式:① an=[1+(-1)n] ② an=③ an= 其中可作为{an}的通项公式的是( )A.①B.①②C.②③D.①②③解:D 例 2. 已知数...