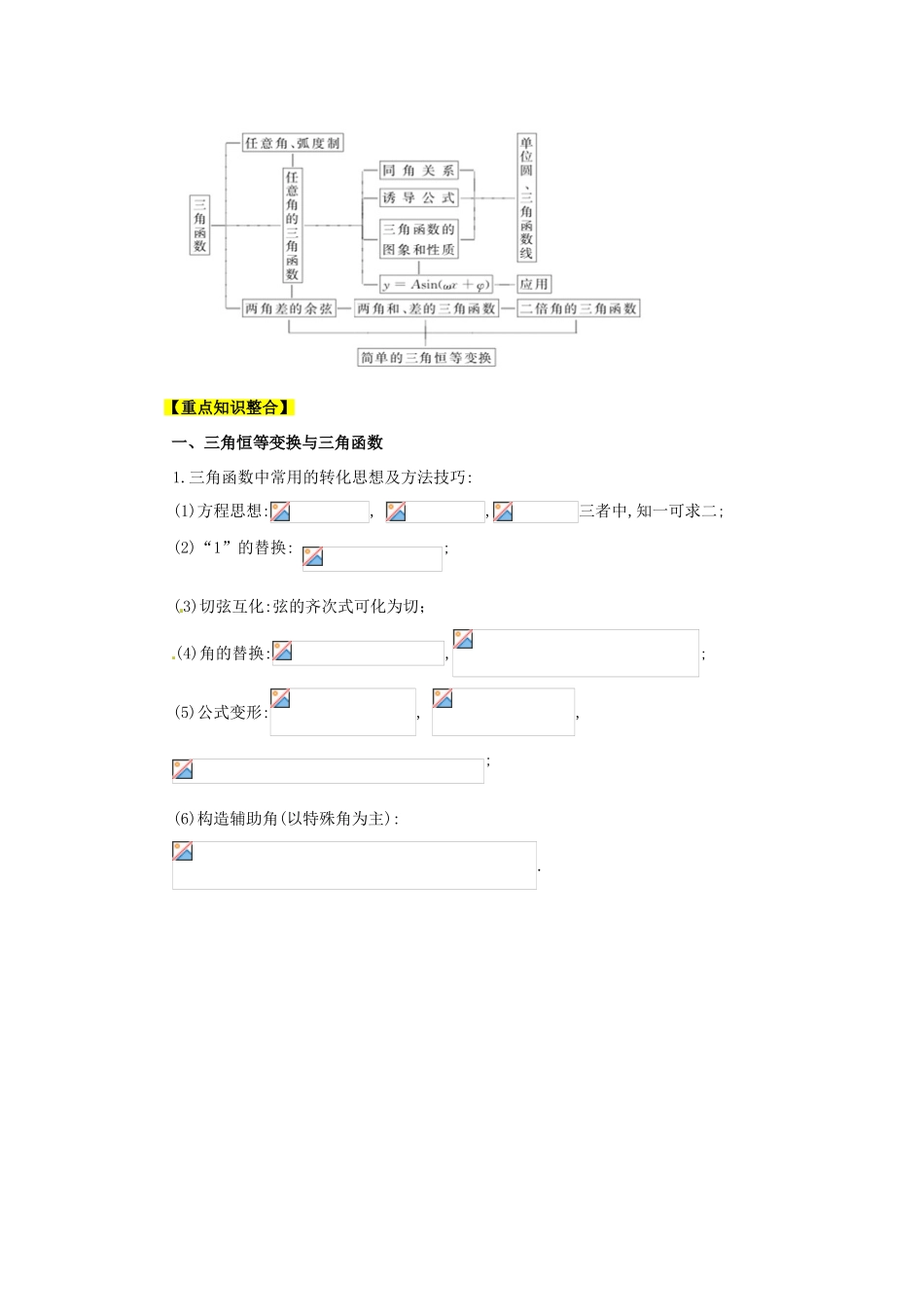
2013 高考数学二轮复习精品资料专题 04 三角函数和解三角形教学案(学生版)【2013 考纲解读】 1.了解任意角的概念,了解弧度制的概念,能进行弧度与角度的互化;理解任意角的三角函数(正弦、余弦、正切)的定义.2.能利用单位圆中的三角函数线推导出,的正弦、余弦、正切的诱导公式;理解同角的三角函数的基本关系式:sin2x+cos2x=1,.3.能画出 y=sinx, y=cosx, y=tanx 的图象,了解三角函数的周期性;2.理解正弦函数,余弦函数在区间[0,2]上的性质(如单调性,最大值和最小值以及与 x 轴的交点等),理解正切函数在区间(-,)内的单调性.4.了解函数的物理意义;能画出的图象,了解对函数图象变化的影响.5.会用向量的数量积推导两角差的余弦公式;能利用两角差的余弦公式导出两角和与差的正弦、余弦和正切公式,了解它们的内在联系.6.能利用两角差的余弦公式导出二倍角的正弦、余弦、正切公式,了解它们的内在联系;能运用上述公式进行简单的恒等变换【知识网络构建】 【重点知识整合】一、三角恒等变换与三角函数1.三角函数中常用的转化思想及方法技巧:(1)方程思想:, ,三者中,知一可求二;(2)“1”的替换: ;(3)切弦互化:弦的齐次式可化为切;(4)角的替换:,;(5)公式变形:, ,;(6)构造辅助角(以特殊角为主):.二、解三角形1.正弦定理已知在△ABC 中,a,b,c 分别为内角 A、B、C 的对边,则===2R(R 为三角形外接圆的半径).2.余弦定理已知在△ABC 中,a,b,c 分别为内角 A、B、C 的对边,则 a2=b2+c2-2bccosA,cosA=,另外两个同样.3.面积公式已知在△ABC 中,a,b,c 分别为内角 A、B、C 的对边,则(1)三角形的面积等于底乘以高的;(2)S=absinC=bcsinA=acsinB=(其中 R 为该三角形外接圆的半径);(3)若三角形内切圆的半径是 r,则三角形的面积 S=(a+b+c)r;(4)若 p=,则三角形的面积 S=.【高频考点突破】【变式探究】已知角 θ 的顶点与原点重合,始边与 x 轴的正半轴重合,终边在直线 y=2x 上,则 cos2θ=( )A.- B.- C. D.【方法技巧】1.用三角函数定义求三角函数值有时反而更简单; 2.同角三角函数间的关系、诱导公式在三角函数式的化简中起着举足轻重的作用,应注意正确选择公式、注意公式的应用条件. 考点二 三角函数的性质 三角函数的单调区间:y=sinx 的递增区间是[2kπ-,2kπ+](k∈Z),递减区间是[2kπ+,2kπ+](k∈Z);y=cosx 的递增区间是[2kπ-π,2kπ](k∈Z),递...