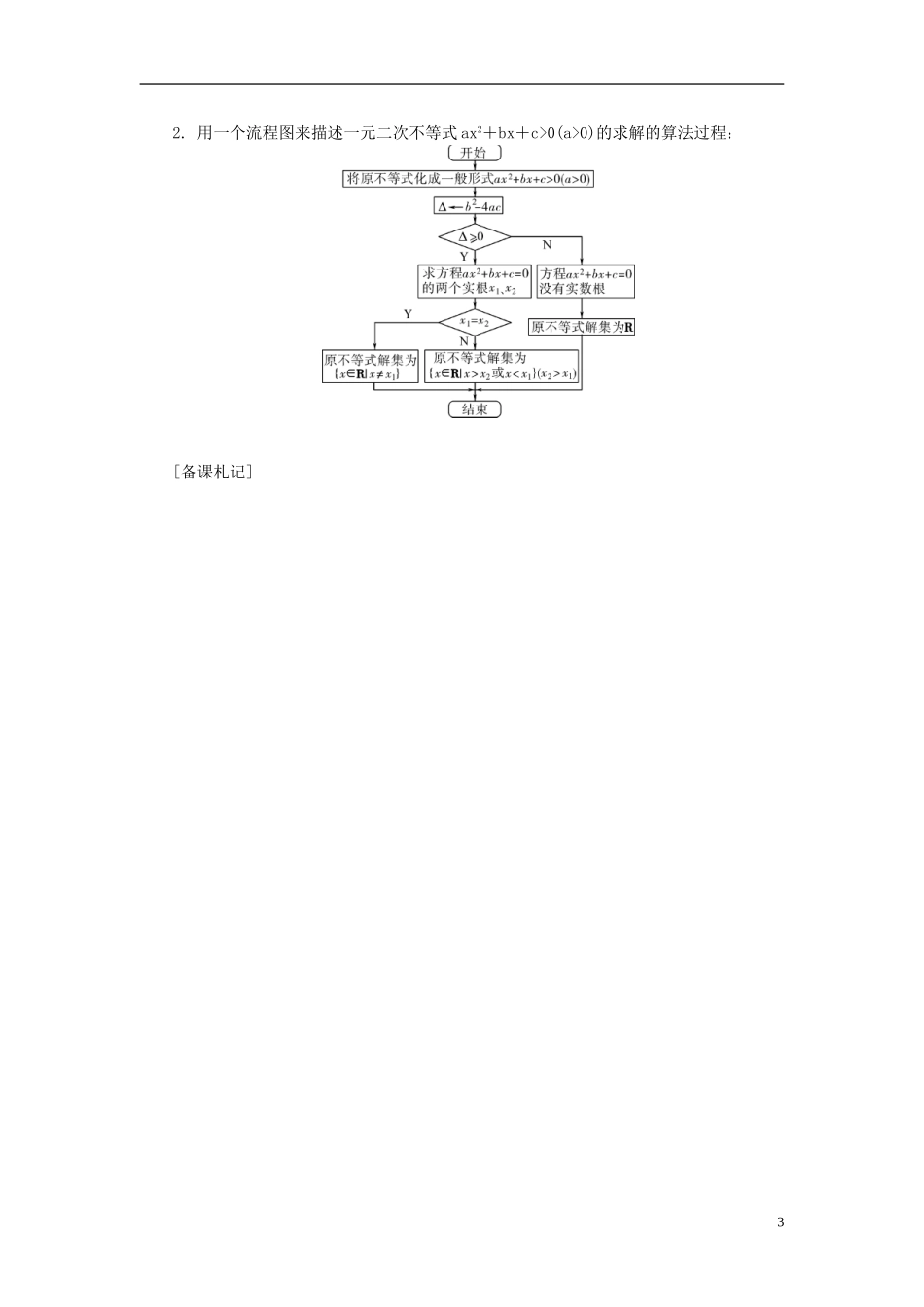
2014 届高三数学总复习 6.1 一元二次不等式及其解法教案 新人教 A 版考情分析考点新知掌握一元二次不等式解法,理解一元二次不等式、一元二次方程、二次函数之间关系并能灵活运用.① 会从实际情境中抽象出一元二次不等式模型;② 通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系;③ 会解一元二次不等式,对给定的一元二次不等式,会设计求解程序框图.1. (必修 5P69习题 2(2)改编)不等式 3x2-x-4≤0 的解集是__________. 答案:解析:由 3x2-x-4≤0,得(3x-4)(x+1)≤0,解得-1≤x≤.2. (必修 5P71习题 1(3)改编)不等式 x2+x-6≤0 的解集为________.答案:[-3,2]解析:由 x2+x-6≤0,得-3≤x≤2.3. (必修 5P71习题 7(4)改编)不等式>0 的解集是________.答案:解析:不等式>0 等价于(1-2x)(x+1)>0,也就是(x+1)<0,所以-10 对一切实数 x 恒成立,则实数 k 的取值范围是________.答案:k>2 或 k<-2解析:由 Δ=4-4(k2-3)<0,知 k>2 或 k<-2.5. (必修 5P71习题 6 改编)不等式 ax2+bx+2>0 的解集是,则 a-b=________.答案:-10解析:由题意可知,-和是方程 ax2+bx+2=0 的两个实根,则 解得,所以 a-b=-10.1. 一元二次不等式的解法在二次函数 y=ax2+bx+c(a≠0)中,令 y=0,得到一元二次方程 ax2+bx+c=0(a≠0).若将等号“=”改为不等号“>”或“<”,便得到一元二次不等式 ax2+bx+c>0(或<0).因此,可以通过 y=ax2+bx+c(a≠0)图象与 x 轴的交点求得一元二次不等式的解,具体如下表:二次函数一元二次方程一元二次不等式一般式y=ax2+bx+c(a>0)Δ=b2-4acax2+bx+c=0(a>0)ax2+bx+c>0(a>0)ax2+bx+c<0(a>0)1图象与解Δ>0x=x1,x=x2xx2x1< x0(a>0)的求解的算法过程:[备课札记]3题型 1 一元二次不等式的解法例 1 已知 a>0,解关于 x 的不等式 x2-x+1<0.解:原不等式可化为(x-a)<0.由 a-=,得①当 0<a<1 时,a<,解集为;②当 a>1 时,a>,解集为;③当 a=1 时,a=,(x-1)2<0 的解集为.已知关于 x 的不等式:<1.(1) 当 a=1 时,解该不等式;(2) 当 a>0 时,解该不等式.解:(1) 当 a...