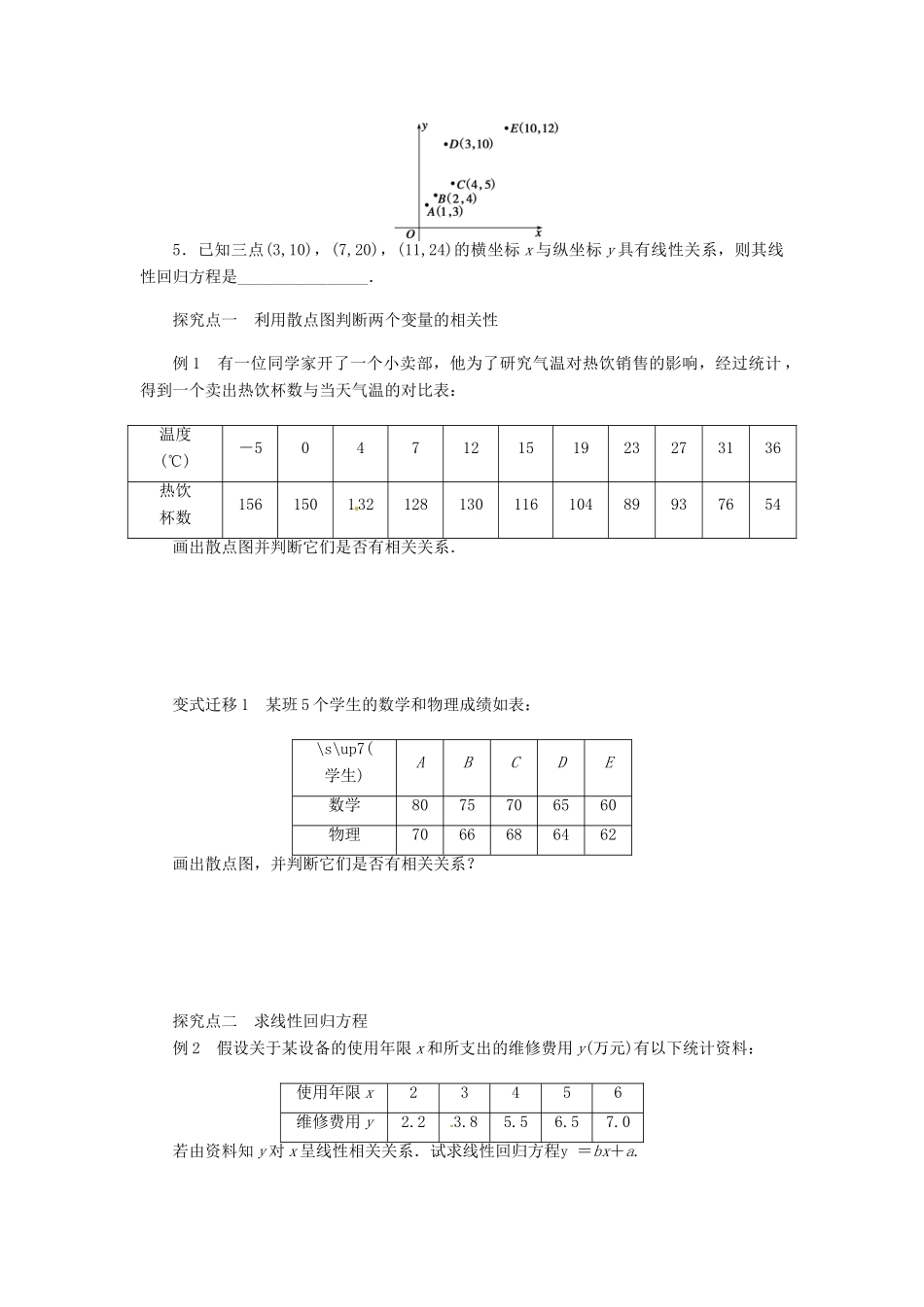
学案 56 线性回归方程导学目标: 1.会作两个有关联变量的数据的散点图,会利用散点图认识变量间的相关关系.2.了解最小二乘法的思想,能根据给出的线性回归方程系数公式建立线性回归方程.自主梳理1.相关关系:两 个变量之间的关系可能是________关系(如:函数关系),或__________关系.当自变量取值一定时,因变量也确定,则为确定性关系;当自变量取值一定时,因变量带有随机性,这种变量之间的关系称为相关关系.相关关系是一种非确定性关系.2.散点图:将各数据在平面直角坐标系中的对应点画出来,得到表示两个变量的一组数据的图形,这样的图形叫做散点图.3.回归直线(1)定义:如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有________________,这条直线叫做回归直线.(2)最小二乘法:通过求 Q=∑ (yi-bxi-a)2的最小值而得出回归直线的方法,即求回归直线,使得样本数据的点到它的距离的平方和______,这一方法叫做最小二乘法.(3)线性回归方程方程y =bx+a 是两个具有线性相关关系的变量的一组数据(x1,y1),(x2,y2),…,(xn,yn)的线性回归方程,其中 a,b 是待定参数..自我检测1.下列有关线性回归的说法,正确的序号是________.① 相关关系的两个变量不一定是因果关系;② 散点图能 直观地反映数据的相关程度;③ 回归直线最能代表线性相关的两个变量之间的关系;④ 任一组数据都有线性回归方程.2.下列关系:① 人的年龄与其拥有的财富之间的关系;②曲线上的点与该点的坐标之间的关系;③苹果的产量与气候之间的关系;④森林中的同一树木,其截面直径与高度之间的关系;⑤学生的身高与其学号之间的关系,其中有相关关系的是________(填序号).3.下表是某厂 1~4 月份用水量(单位:百吨)的一组数据:月份 x1234用水量 y4.5432.5由散点图可知,用水量 y 与月份 x 之间有较好的 线性相关关系,其线性回归方程是y =-0.7x+a,则 a=________.4.如图所示,有 5 组(x,y)数据,去掉________组数据后,剩下的 4 组数据的线性相关性最大.5.已知三点(3,10),(7,20),(11,24)的横坐标 x 与纵坐标 y 具有线性关系,则其线性回归方程是________________.探究点一 利用散点图判断两个变量的相关性例 1 有一位同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计 ,得到一个卖出热饮杯数与当天气温的对比表:温度(℃)-504712151923273136热饮...