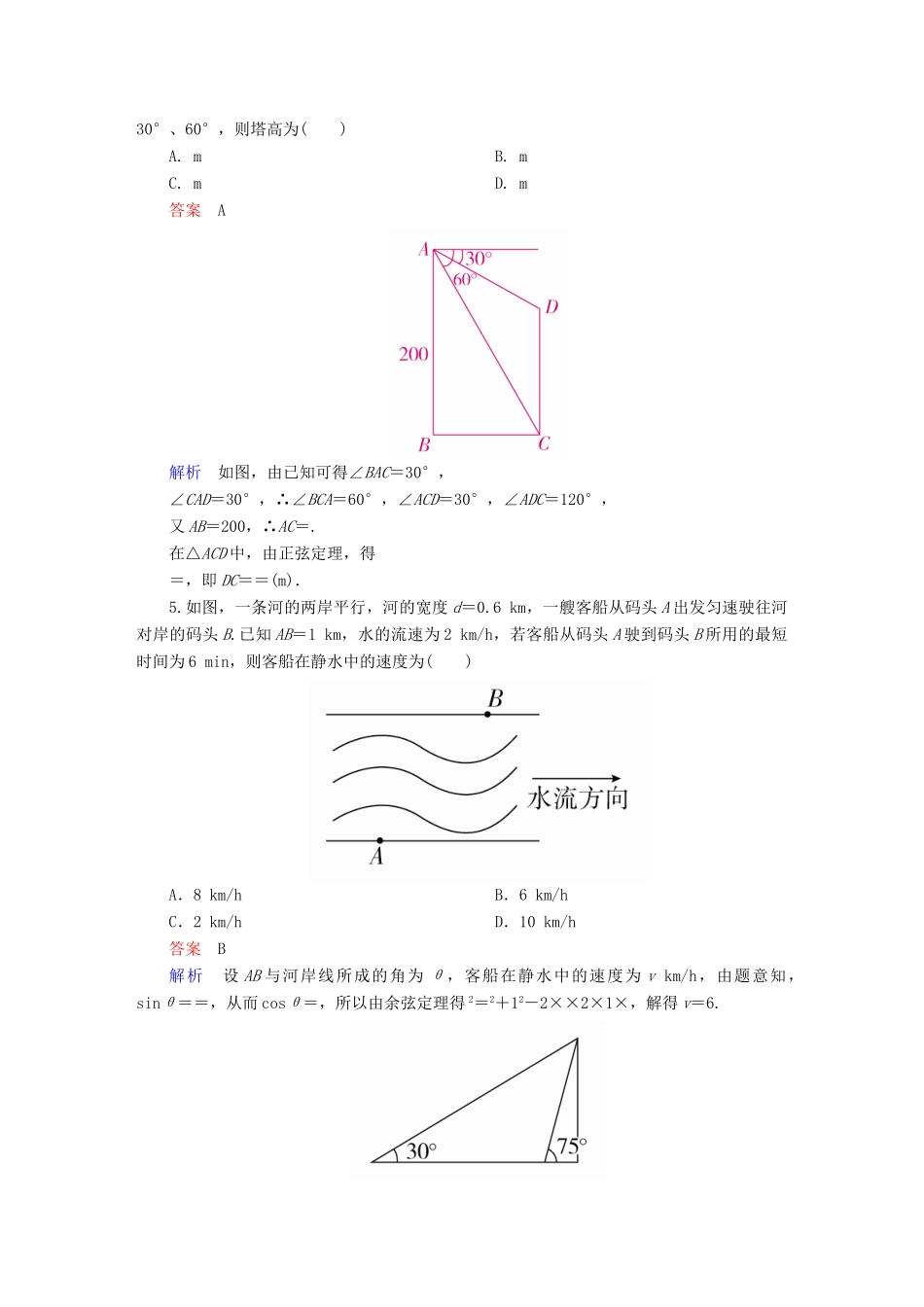
第7讲解三角形的应用举例板块四模拟演练·提能增分[A级基础达标]1.已知A,B两地间的距离为10km,B,C两地间的距离为20km,现测得∠ABC=120°,则A,C两地间的距离为()A.10kmB.10kmC.10kmD.10km答案D解析如图所示,由余弦定理可得:AC2=100+400-2×10×20×cos120°=700,∴AC=10(km).2.[2018·武汉模拟]海面上有A,B,C三个灯塔,AB=10nmile,从A望C和B成60°视角,从B望C和A成75°视角,则BC=()A.10nmileB.nmileC.5nmileD.5nmile答案D解析由题意可知,∠CAB=60°,∠CBA=75°,所以∠C=45°,由正弦定理得=,所以BC=5.3.如图所示,已知两座灯塔A和B与海洋观察站C的距离都等于akm,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与灯塔B的距离为()A.akmB.akmC.akmD.2akm答案B解析在△ABC中,由余弦定理得AB2=AC2+BC2-2AC·BC·cos∠ACB=a2+a2-2a2cos120°=3a2,故|AB|=a.4.[2018·临沂质检]在200m高的山顶上,测得山下一塔顶与塔底俯角分别为30°、60°,则塔高为()A.mB.mC.mD.m答案A解析如图,由已知可得∠BAC=30°,∠CAD=30°,∴∠BCA=60°,∠ACD=30°,∠ADC=120°,又AB=200,∴AC=.在△ACD中,由正弦定理,得=,即DC==(m).5.如图,一条河的两岸平行,河的宽度d=0.6km,一艘客船从码头A出发匀速驶往河对岸的码头B.已知AB=1km,水的流速为2km/h,若客船从码头A驶到码头B所用的最短时间为6min,则客船在静水中的速度为()A.8km/hB.6km/hC.2km/hD.10km/h答案B解析设AB与河岸线所成的角为θ,客船在静水中的速度为vkm/h,由题意知,sinθ==,从而cosθ=,所以由余弦定理得2=2+12-2××2×1×,解得v=6.6.如图,某工程中要将一长为100m,倾斜角为75°的斜坡改造成倾斜角为30°的斜坡,并保持坡高不变,则坡底需加长________m.答案100解析设坡底需加长xm,由正弦定理得=,解得x=100.7.如图,为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为________km.答案7解析 82+52-2×8×5×cos(π-D)=32+52-2×3×5×cosD,∴cosD=-.∴AC==7(km).8.[2018·河南调研]如图,在山底A点处测得山顶仰角∠CAB=45°,沿倾斜角为30°的斜坡走1000米至S点,又测得山顶仰角∠DSB=75°,则山高BC为________米.答案1000解析由题图知∠BAS=45°-30°=15°,∠ABS=45°-(90°-∠DSB)=30°,∴∠ASB=135°,在△ABS中,由正弦定理可得=,∴AB=1000,∴BC==1000(米).9.[2018·山西监测]如图,点A,B,C在同一水平面上,AC=4,CB=6.现要在点C处搭建一个观测站CD,点D在顶端.(1)原计划CD为铅垂线方向,α=45°,求CD的长;(2)搭建完成后,发现CD与铅垂线方向有偏差,并测得β=30°,α=53°,求CD2.(结果精确到1)(本题参考数据:sin97°≈1,cos53°≈0.6)解(1) CD为铅垂线方向,点D在顶端,∴CD⊥AB.又 α=45°,∴CD=AC=4.(2)在△ABD中,α+β=53°+30°=83°,AB=AC+CB=4+6=10,∴∠ADB=180°-83°=97°,∴由=得AD===≈5.在△ACD中,CD2=AD2+AC2-2AD·ACcosα=52+42-2×5×4×cos53°≈17.10.如图,在海岸A处发现北偏东45°方向,距A处(-1)海里的B处有一艘走私船.在A处北偏西75°方向,距A处2海里的C处的我方缉私船奉命以10海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.解设缉私船应沿CD方向行驶t小时,才能最快截获(在D点)走私船,则CD=10t海里,BD=10t海里,在△ABC中,由余弦定理,有BC2=AB2+AC2-2AB·AC·cos∠BAC=(-1)2+22-2(-1)×2×cos120°=6,解得BC=.又 =,∴sin∠ABC===,∴∠ABC=45°,故B点在C点的正东方向上,∴∠CBD=90°+30°=120°,在△BCD中,由正弦定理,得=,∴sin∠BCD===.∴∠BCD=30°,∴缉私船沿北偏东60°的方向行驶.又在△BCD中,∠CBD=120°,∠BCD=30°,∴∠D=30°,∴BD=BC,即...