2014高考数学一轮总复习 5.1 任意角的三角函数的概念教案 理 新人教A版VIP专享

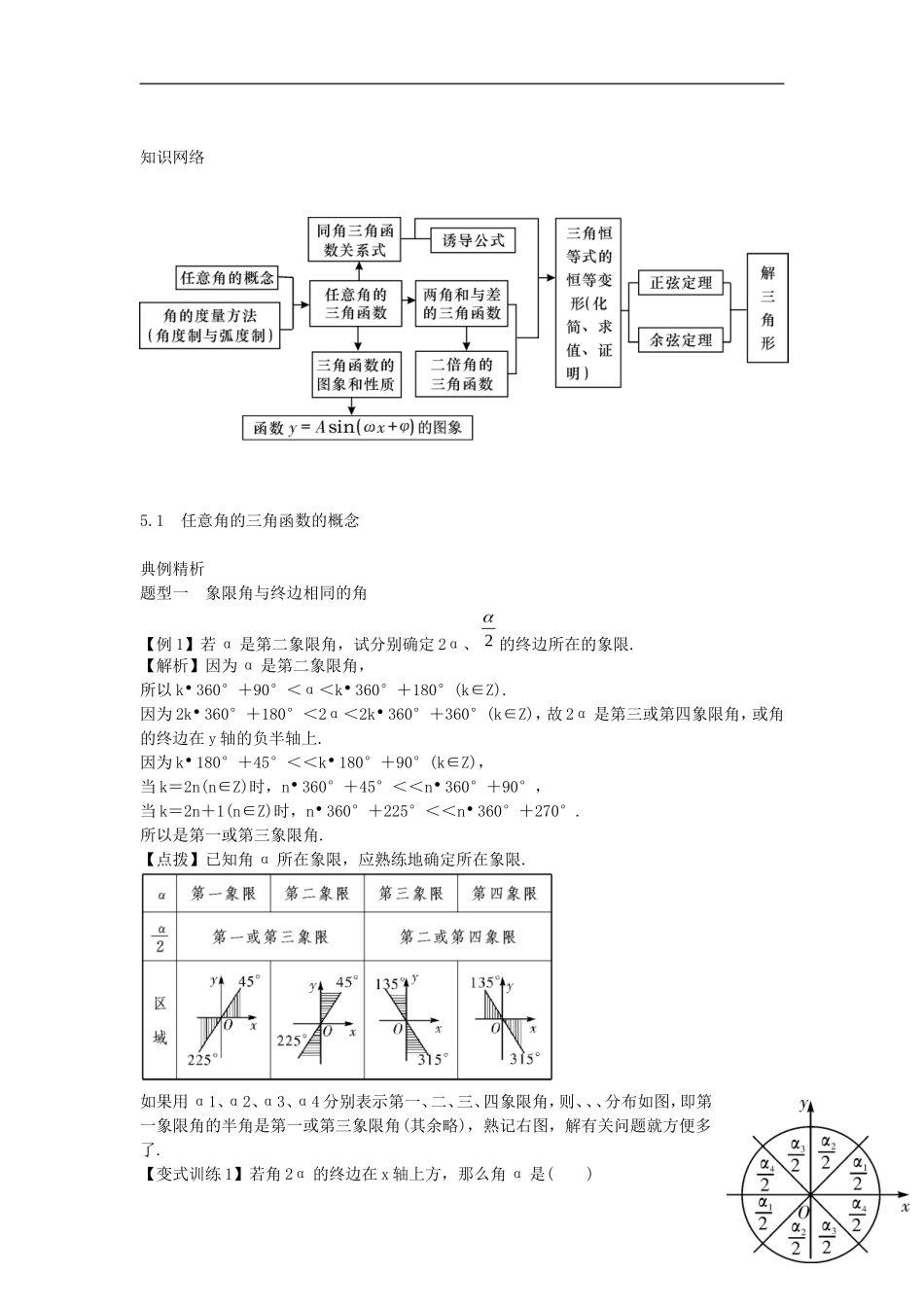
第五章 三角函数高考导航考试要求重难点击命题展望 1.了解任意角的概念和弧度制的概念，能进行弧度与角度的互化.2.理解任意角三角函数(正弦、余弦、正切)的定义.3.能利用单位圆中的三角函数线推导出2π，π±α 的正弦、余弦、正切的诱导公式，能画出y＝sin x， y＝cos x ， y＝tan x 的图象，了解三角函数的周期性.4.理解正弦函数、余弦函数在[0,2π]上的性质(如单调性、最大值和最小值、图象与 x 轴的交点等)，理解正切函数在(－ 2π, 2π)上的单调性.5.理解同角三角函数的基本关系式：sin2x＋cos2x＝1 ，xxcossin＝tan x.6.了解函数 y＝Asin(ωx＋φ)的物理意义，能画出函数 y＝Asin(ωx＋φ)的图象，了解参数A，ω，φ 对函数图象变化的影响.7.会用三角函数解决一些简单实际问题，体会三角函数是描述周期变化现象的重要函数模型.8.会用向量的数量积推导出两角差的余弦公式，会用两角差的余弦公式推导出两角和的正弦、余弦、正切公式和二倍角的正弦、余弦、正切公式，了解它们的内在联系，能运用上述公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式，但不要求记忆).9.掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题，能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.本章重点：1.角的推广，三角函数的定义，诱导公式的运用；2.三角函数的图象与性质，y＝Asin(ωx＋)(ω ＞ 0) 的 性质 、 图 象 及 变换；3.用三角函数模型解决实际问题；4.以和、差、倍角公式为依 据 ， 提 高 推理、运算能力；5.正、余弦定理及应用.本章难点：1.任意角的三角函数的几何表示，图象变换与函数解析式变换的内在联系；2.灵活运用 三 角 公 式 化简、求值、证明； 3.三角函数的奇偶性、单调性的判断，最值的求法；4.探索两角差的余弦公式；5.把实际问题转化为三角函数问题. 三角函数是基本初等函数，是描述周期现象的重要数 学 模 型 . 三角 函 数 的 概念、图象和性质是高考数学必考的基础知识 之 一 . 在 高考中主要考查对三角函数概念的理解；运用函数公式进行恒等变形、化简、求值、证明三角函数的图象和性质以及图象变换、作图、识图等.解三角形的问题往往与其他知 识 ( 如 立 体几何、解析几何、向量等)相联系，考查考生的数学应用意识，体现以能力立意的高考命题原则.1知识网络 5.1 任意角的三角函数的概念典例精析题型一 象限...