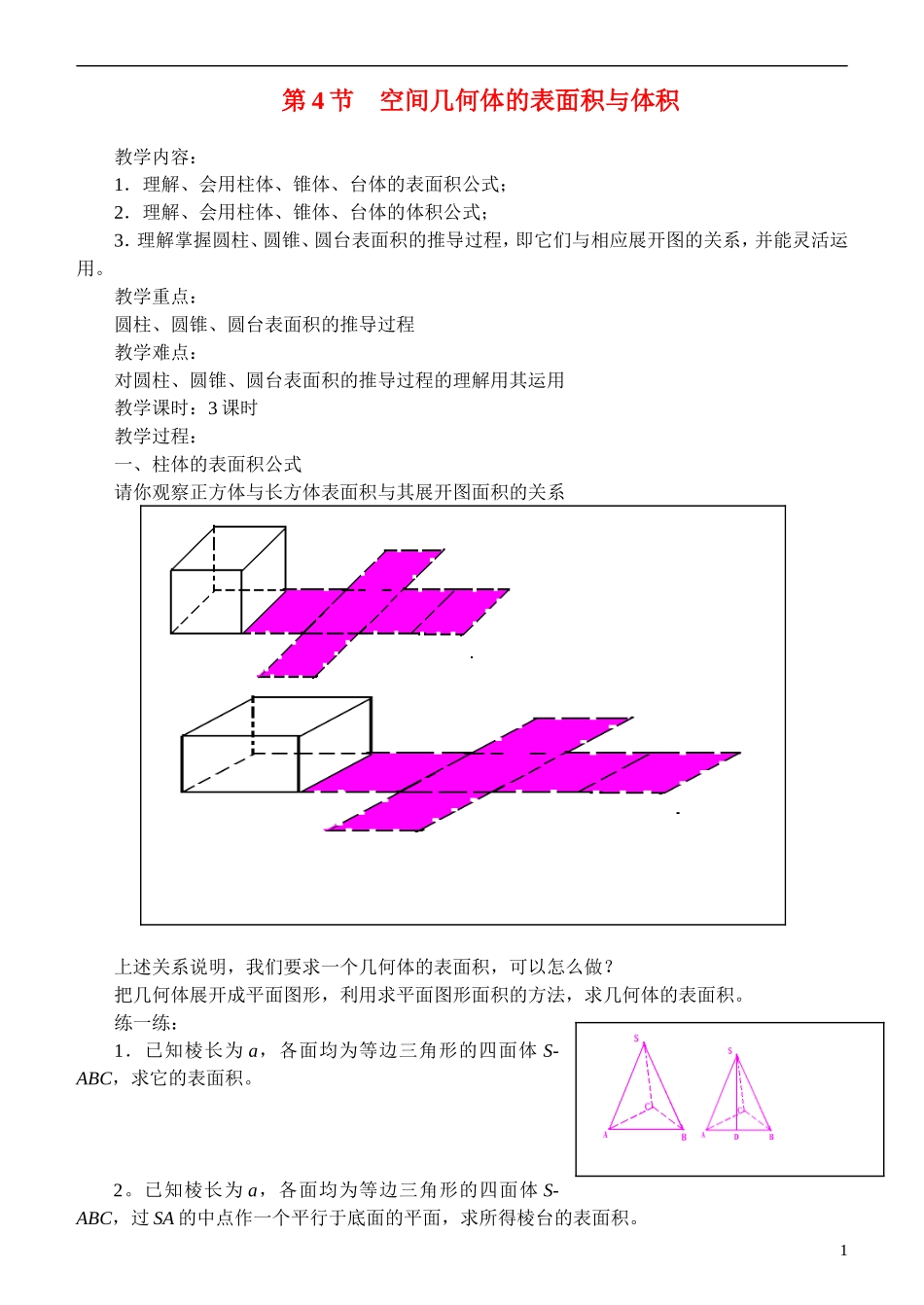
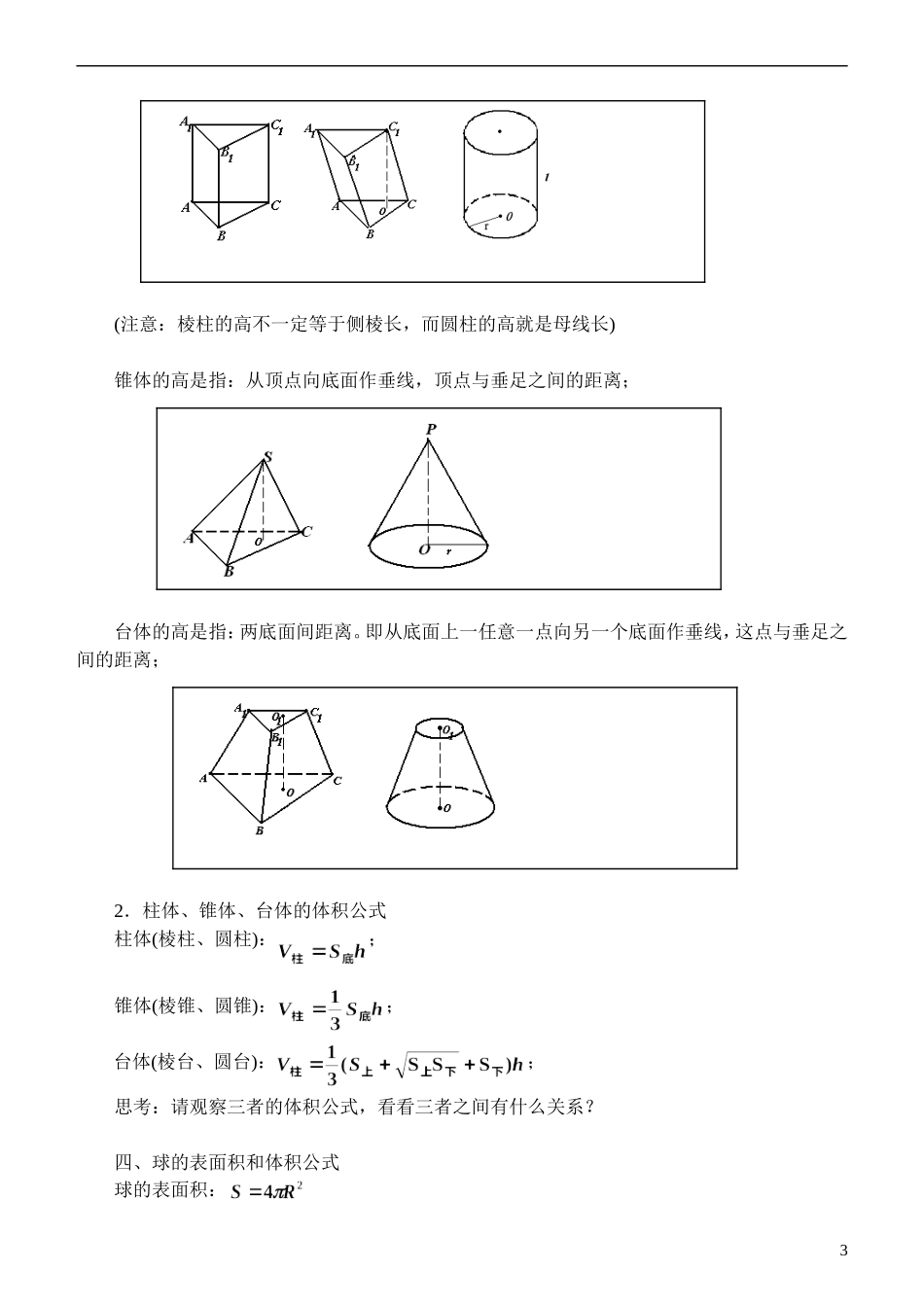
第 4 节 空间几何体的表面积与体积 教学内容:1.理解、会用柱体、锥体、台体的表面积公式;2.理解、会用柱体、锥体、台体的体积公式;3.理解掌握圆柱、圆锥、圆台表面积的推导过程,即它们与相应展开图的关系,并能灵活运用。教学重点:圆柱、圆锥、圆台表面积的推导过程教学难点:对圆柱、圆锥、圆台表面积的推导过程的理解用其运用教学课时:3 课时教学过程:一、柱体的表面积公式请你观察正方体与长方体表面积与其展开图面积的关系上述关系说明,我们要求一个几何体的表面积,可以怎么做?把几何体展开成平面图形,利用求平面图形面积的方法,求几何体的表面积。练一练:1.已知棱长为 a,各面均为等边三角形的四面体 S-ABC,求它的表面积。2。已知棱长为 a,各面均为等边三角形的四面体 S-ABC,过 SA 的中点作一个平行于底面的平面,求所得棱台的表面积。1(说明:此处介绍中截面的概念及面积的比等于相似比的平方)二、动手试一试:看看圆柱、圆锥、圆台的展开图是什么形状?可以看出:1.圆柱展开图是矩形,那么其长、宽分别对应圆柱的什么?2.圆锥展开图是扇形,那么其半径、弧长分别对应圆锥的什么?3.圆台展开图是圆环,那么其圆环的宽度、内弧长、外弧长分别对应圆台的什么?上述三者各自的表面积是多少?;;(说明:此处介绍扇形面积公式)练一练:已知圆锥的表面积为 a,且它的侧面展开图是个半圆,求这个圆锥的底面直径。解:设圆锥底面圆的半径为 r,母线长为 l,则 解得 , 即圆锥底面的直径为第一小节到此结束三、柱体、锥体、台体的体积公式1.柱体、锥体、台体的高的概念柱体的高是指:两底面间距离。即从底面上一任意一点向另一个底面作垂线,这点与垂足之间的距离;2(注意:棱柱的高不一定等于侧棱长,而圆柱的高就是母线长)锥体的高是指:从顶点向底面作垂线,顶点与垂足之间的距离;台体的高是指:两底面间距离。即从底面上一任意一点向另一个底面作垂线,这点与垂足之间的距离;2.柱体、锥体、台体的体积公式柱体(棱柱、圆柱):;锥体(棱锥、圆锥):;台体(棱台、圆台):;思考:请观察三者的体积公式,看看三者之间有什么关系?四、球的表面积和体积公式球的表面积:3 球的体积:练一练:1.正方形边长扩大 n 倍,其面积扩大____倍;正方体棱长扩大 n 倍,其表面积扩大____倍,体积扩大_____倍;2.圆的半径扩大 n 倍,其面积扩大____倍;球半径扩大 n 倍,其表面积扩大____倍,体积扩大____...