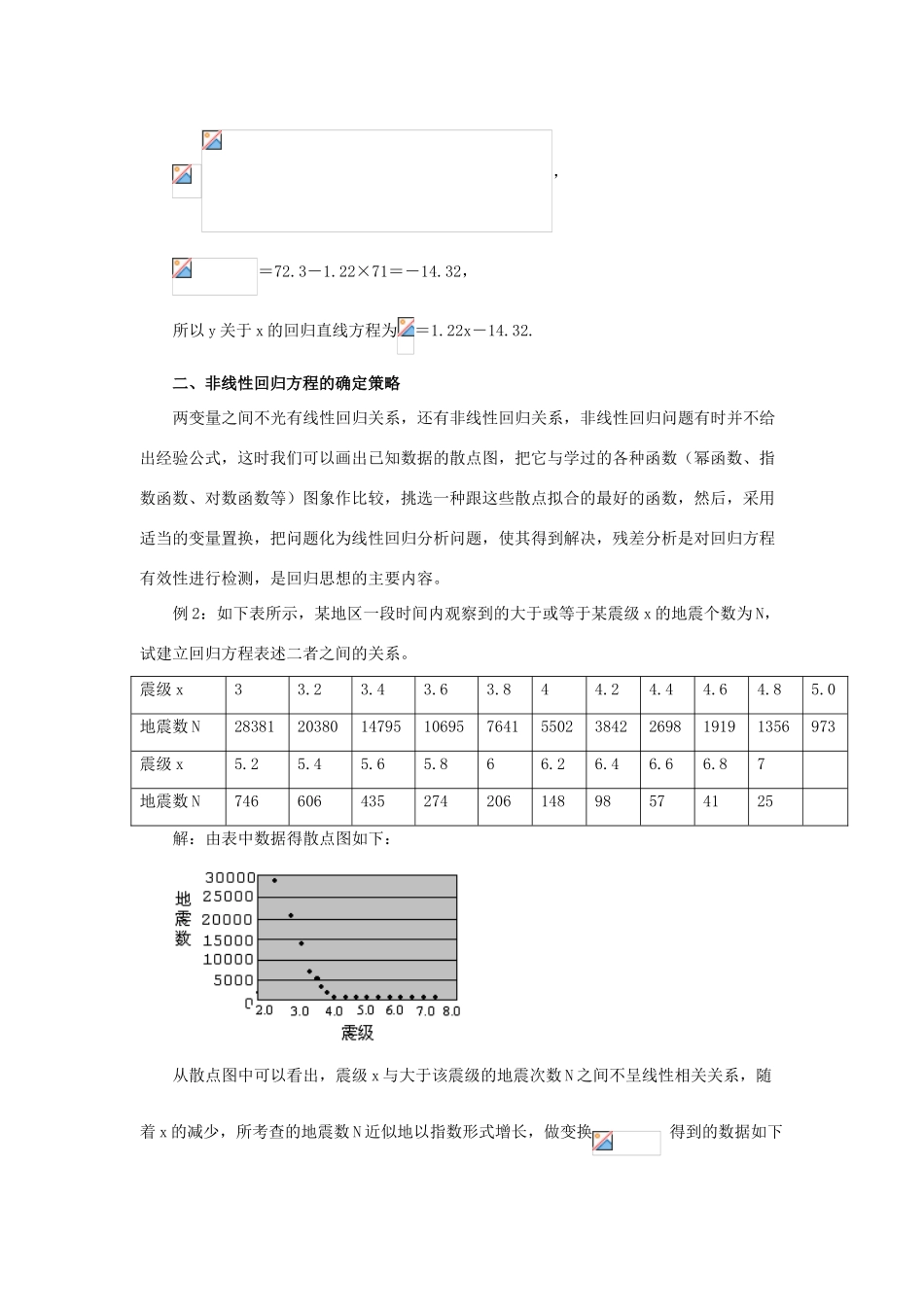
两种回归方程的求解策略准确确定回归直线方程,有利与进一步加强数学应用意识,培养运用所学知识解决实际问题的能力,正确的求出回归直线方程也是本节的重点。一、线性回归方程的确定策略线性回归方程的确定主要策略有:通过散点图来描述出变量间的图形;或利用样本相关关系数 r 来判断两个变量之间是否具有线性相关关系时,可以依据|r|>0.75 时,我们认为有很强的线性相关关系,可以求回归直线方程。例 1、10 名同学在高一和高二的数学成绩如下表:x74717268767367706574Y76757170767965776272其中 x 为高一数学成绩,y 为高二数学成绩。(1)y 与 x 是否具有相关关系;(2)如果 y 与 x 是相关关系,求回归直线方程。解(1)由已知表格中的数据,利用计算器进行计算得,,,,。,.r=由于,由 0.780 297>0.75,知,有很大的把握认为 x 与 y 之间具有线性相关关系。 (2)y 与 x 具有线性相关关系,设回归直线方程=a+bx,则,=72.3-1.22×71=-14.32,所以 y 关于 x 的回归直线方程为=1.22x-14.32.二、非线性回归方程的确定策略两变量之间不光有线性回归关系,还有非线性回归关系,非线性回归问题有时并不给出经验公式,这时我们可以画出已知数据的散点图,把它与学过的各种函数(幂函数、指数函数、对数函数等)图象作比较,挑选一种跟这些散点拟合的最好的函数,然后,采用适当的变量置换,把问题化为线性回归分析问题,使其得到解决,残差分析是对回归方程有效性进行检测,是回归思想的主要内容。例 2:如下表所示,某地区一段时间内观察到的大于或等于某震级 x 的地震个数为 N,试建立回归方程表述二者之间的关系。震级 x33.23.43.63.844.24.44.64.85.0地震数 N28381203801479510695764155023842269819191356973震级 x5.25.45.65.866.26.46.66.87地震数 N74660643527420614898574125解:由表中数据得散点图如下:从散点图中可以看出,震级 x 与大于该震级的地震次数 N 之间不呈线性相关关系,随着 x 的减少,所考查的地震数 N 近似地以指数形式增长,做变换 得到的数据如下表所示.x33.23.43.63.844.24.44.64.85.0y4.4534.3094.1704.0293.8833.7413.5853.4313.2833.1322.988x5.25.45.65.866.26.46.66.87y2.8732.7812.6382.4382.3142.1701.9911.7561.6131.398x 和 y 的散点图如下:从这个散点图中可以看出 x 和 y 之间有很强的线性相关关系,因此可以用线性回归模型拟和它们之间的关系。根据截距和斜率的最小二乘计算公式,得, 故线性回归方程为相关指数,说明 x 可以解释 y 的 99.7%的变化。因此,可以用回归方程描述 x 和 N 之间的关系。