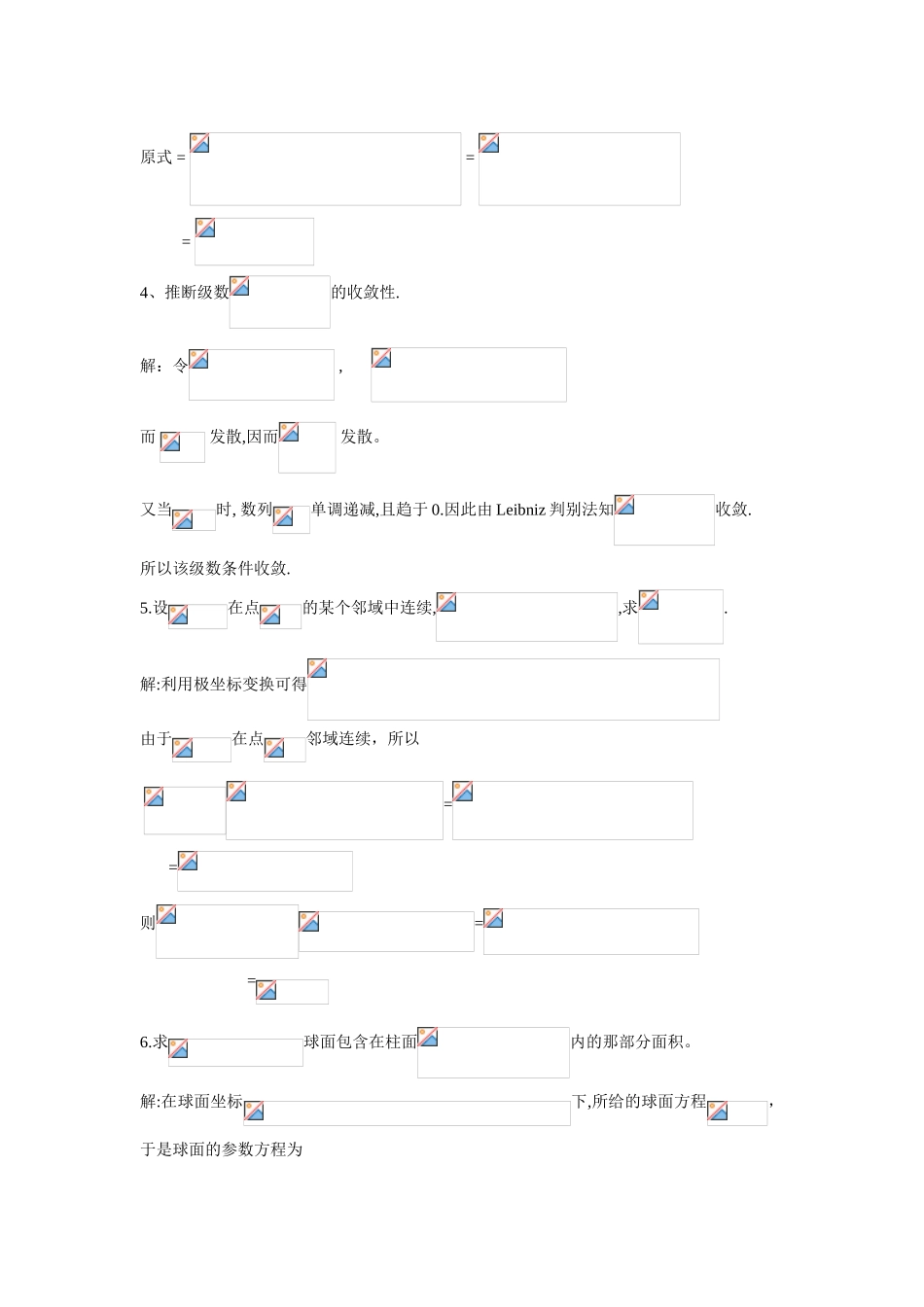
中国科学院数学与系统科学讨论院2024 年硕士讨论生招生初试试题及其解答----博士家园 http://www.bossh.net 计算解:L’Hospital 法则得原式=1、 设证明证:令 (不妨设 ),则所证明的不等式可写成 设 则有 因此在上严格递增,从而对任意,有,即设 则 因 此 对 任 意有 即 .2、 求解:,考虑函数,它在[0,1]上连续,把[0,1]分成 n 等份,分点为,在每一小区间中取,则有.于是,原式 = = = 4、推断级数的收敛性.解:令 , 而 发散,因而 发散。又当时, 数列单调递减,且趋于 0.因此由 Leibniz 判别法知收敛.所以该级数条件收敛.5.设在点的某个邻域中连续,,求.解:利用极坐标变换可得由于在点邻域连续,所以 = =则==6.求球面包含在柱面内的那部分面积。解:在球面坐标下,所给的球面方程,于是球面的参数方程为 其中.那么 所以 又球面的面积为它在第一卦限部分面积的 4 倍,所以.7. 设, 其 中, 且在的 某 个 邻 域 中 满 足.证明在处可微,但函数在(0,0)处不可微. (在处可微性未证明)证:, 考察极限 = 当动点(x,y)沿直线趣于时,显然对不同的 k 有不同的极限值 。因此上述极限不存在,即在点,不能表成故在点不可微分。8.设在上有连续导数,并且,令证明在处三次可微,并求 (右导数)证:利用球面坐标变换得==又在上有连续导数,则 也连续,因此有, 且在上连续,则有 。那么由导数定义知在处三阶可导,且 =.9.设在有限区间上可微,且满足(此处和分别表示在 a 和 b 处的右导数和左导数),则存在 。证:设则在上可微,且 不妨设,则存在且 因在上可导,所以连续.由最值定理知,存在一点最大.由(1)式可知 则是的极大值点,所以有 即 .10. 设,求,并证明 其中 r 是某个大于e 的常数. (未给出证明)解:令有.在处分别对等式两边求一,二,三阶导数可得