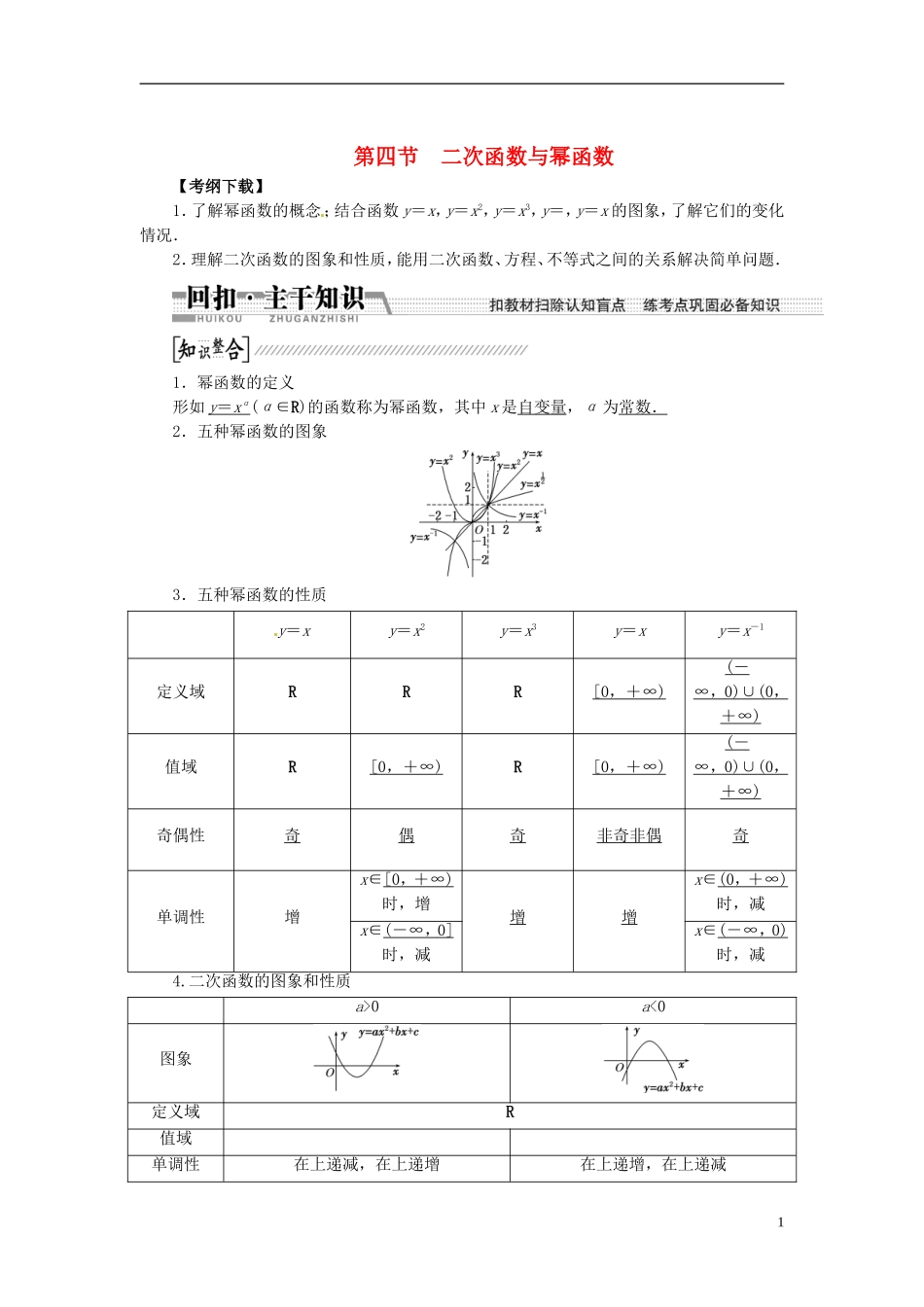
第四节 二次函数与幂函数【考纲下载】1.了解幂函数的概念;结合函数 y=x,y=x2,y=x3,y=,y=x 的图象,了解它们的变化情况.2.理解二次函数的图象和性质,能用二次函数、方程、不等式之间的关系解决简单问题.1.幂函数的定义形如 y = x α (α∈R)的函数称为幂函数,其中 x 是自变量,α 为常数.2.五种幂函数的图象3.五种幂函数的性质y=xy=x2y=x3y=xy=x-1定义域RRR[0 ,+∞ ) ( - ∞, 0) ∪ (0 , +∞ ) 值域R[0 ,+∞ ) R[0 ,+∞ ) ( - ∞, 0) ∪ (0 , +∞ ) 奇偶性奇偶奇非奇非偶奇单调性增x∈[0 ,+∞ ) 时,增增增x∈(0 ,+∞ ) 时,减x∈( -∞, 0] 时,减x∈( -∞, 0) 时,减4.二次函数的图象和性质a>0a<0图象定义域R值域单调性在上递减,在上递增在上递增,在上递减1奇偶性b=0 时为偶函数,b≠0 时为非奇非偶函数图象特点① 对称轴:x=-;②顶点:1.函数 y=(x+1)3,y=x3+1,y=都是幂函数吗?提示:y=(x+1)3与 y=x3+1 不是幂函数;y=是幂函数.2.幂函数的图象能出现在第四象限吗?提示:不能.因为当 x>0 时,根据幂运算,幂函数 y=xα>0 恒成立,所以幂函数在第四象限没有图象.3.ax2+bx+c>0(a≠0)与 ax2+bx+c<0(a≠0)恒成立的条件分别是什么?提示:(1)ax2+bx+c>0(a≠0)恒成立的充要条件是(2)ax2+bx+c<0(a≠0)恒成立的充要条件是1.已知点 M 在幂函数 f(x)的图象上,则 f(x)的表达式为( )A.f(x)=x2 B.f(x)=x-2 C.f(x)=x D.f(x)=x解析:选 B 设 f(x)=xα,则 3=α,∴α=-2.即 f(x)=x-2.2.(教材习题改编)如图中曲线是幂函数 y=xn在第一象限的图象.已知 n 取±2,±四个值,则相应于曲线 C1,C2,C3,C4的 n 值依次为( )A.-2,-,,2 B.2,,-,-2C.-,-2,2, D.2,,-2,-解析:选 B 由幂函数图象及其单调性之间的关系可知,曲线 C1,C2,C3,C4所对应的 n 依次为 2,,-,-2.3.函数 f(x)=(m-1)x2+2mx+3 为偶函数,则 f(x)在区间(-5,-3)上( )A.先减后增 B.先增后减 C.单调递减 D.单调递增解析:选 D 因为 f(x)=(m-1)x2+2mx+3 为偶函数,所以 2m=0,即 m=0.所以 f(x)=-x2+3.由二次函数的单调性可知,f(x)=-x2+3 在(-5,-3)上为增函数.4.已知 f(x)=4x2-mx+5 在[2,+∞)上是增函数,则实数 m ...