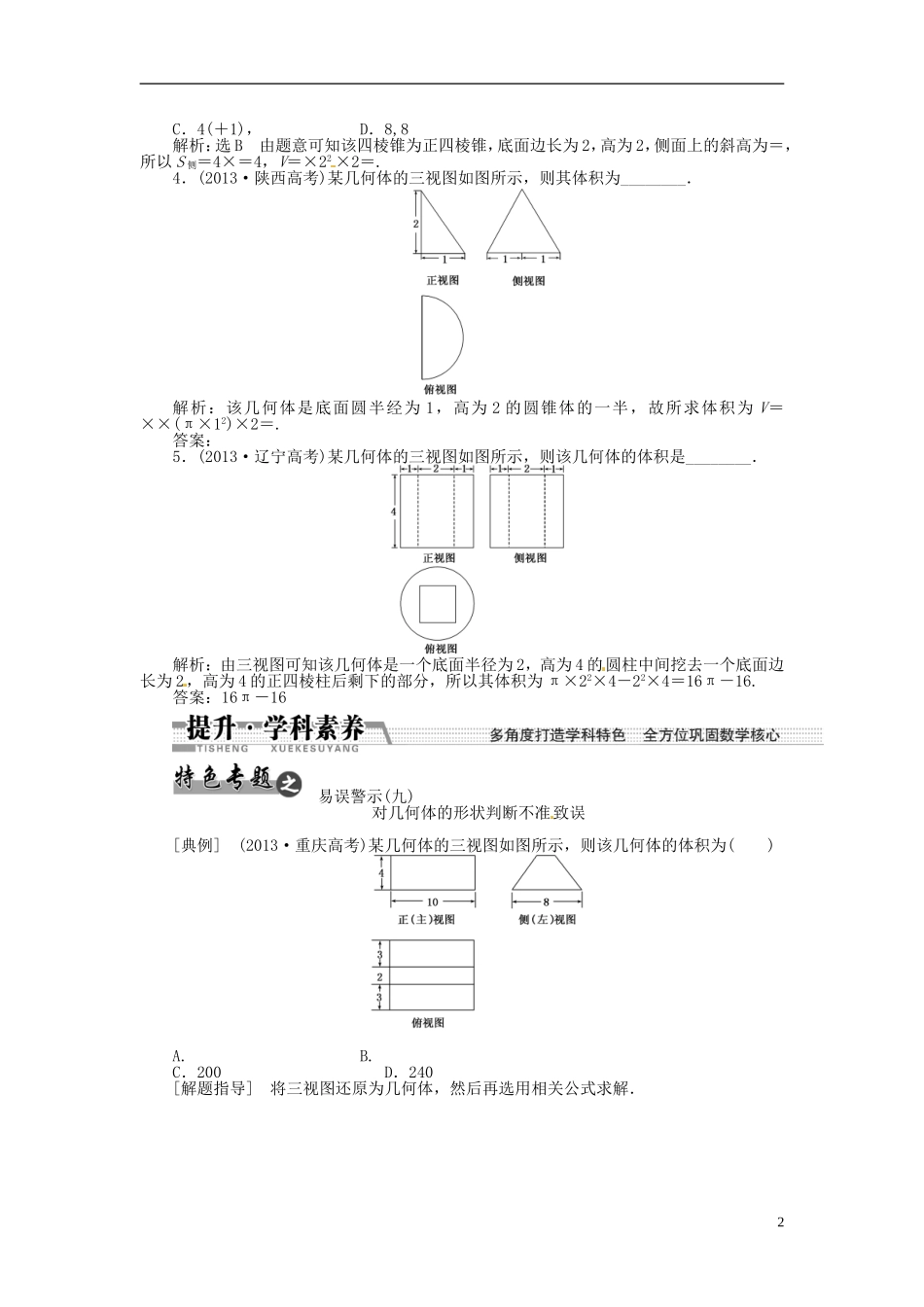
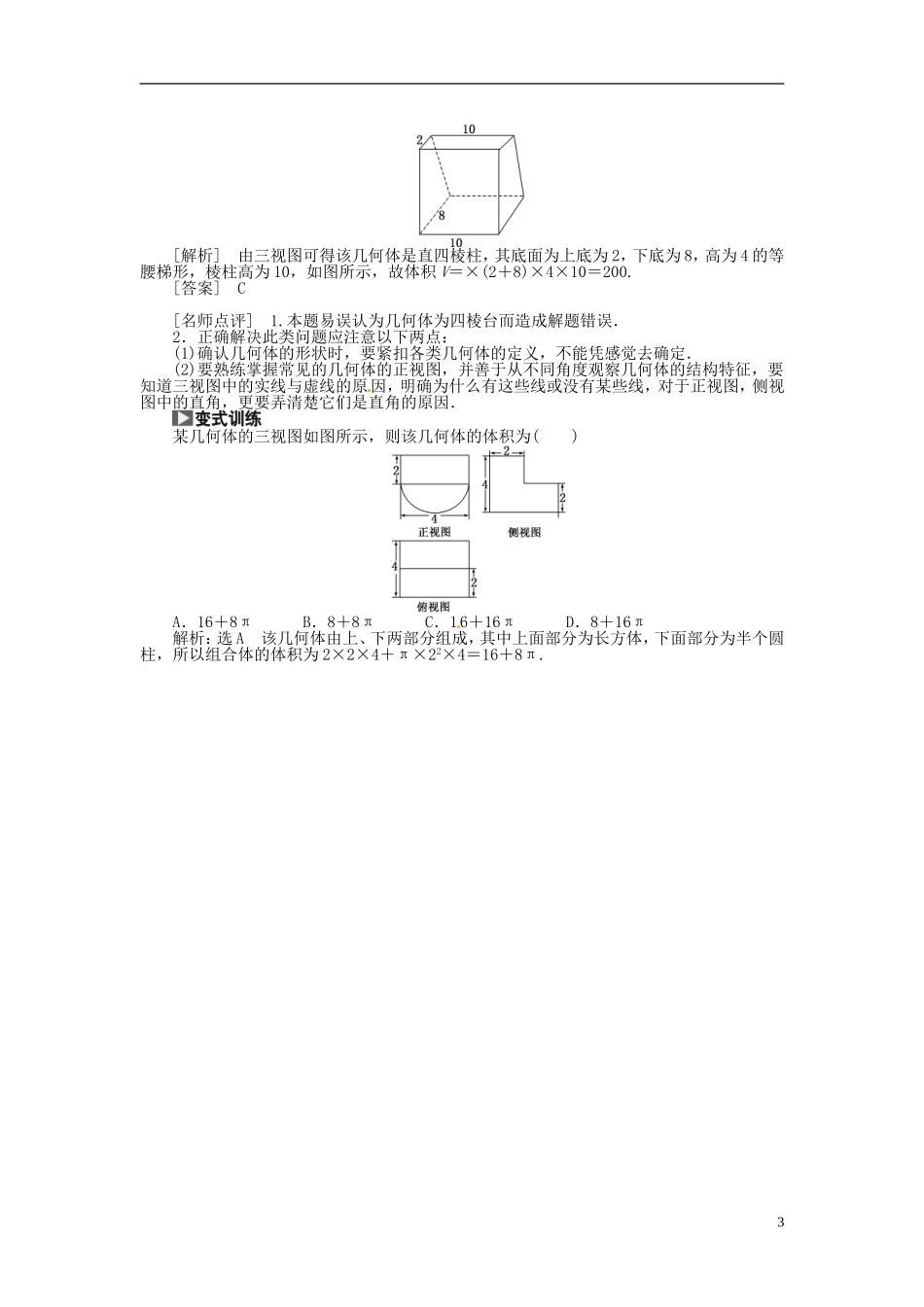
第二节 空间几何体的表面积和体积【考纲下载】了解球体、柱体、锥体、台体的表面积和体积的计算公式(不要求记忆公式).1.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧=2π rl S 圆锥侧=π rl S 圆台侧=π(r+r′)l2.多面体的侧面积和表面积因为多面体的各个面都是平面,所以多面体的侧面积就是侧面展开图的面积,表面积是侧面积与底面积的和.3.空间几何体的表面积和体积公式 名称几何体 表面积体积柱体(棱柱和圆柱)S 表面积=S 侧+2S 底V=Sh锥体(棱锥和圆锥)S 表面积=S 侧+S 底V=Sh台体(棱台和圆台)S 表面积=S 侧+S 上+S 下V=(S 上+S 下+)h球S=4π R 2 [ V=πR3将圆柱、圆锥、圆台的侧面沿任意一条母线剪开铺平,分别得到什么图形?提示:分别得到矩形、扇形、扇环.1.一个正方体的体积是 8,则这个正方体的内切球的表面积是 ( )A.8π B.6π C.4π D.π解析:选 C 设正方体的棱长为 a,则 a3=8,即 a=2.故该正方体的内切球的半径 r=1,所以该正方体的内切球的表面积 S=4πr2=4π.2.直角三角形两直角边 AB=3,AC=4,以 AB 为轴旋转一周所得的几何体的体积为( )A.12π B.16π C.9π D.24π解析:选 B 以 AB 为轴旋转一周所得到的几何体为圆锥,且底面圆的半径为 4,圆锥的高为 3.故体积 V=×π×42×3=16π.3. (2013·山东高考)一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,则该四棱锥侧面积和体积分别是 ( )A.4,8 B.4,1C.4(+1), D.8,8解析:选 B 由题意可知该四棱锥为正四棱锥,底面边长为 2,高为 2,侧面上的斜高为=,所以 S 侧=4×=4,V=×22 ×2=.4.(2013·陕西高考)某几何体的三视图如图所示,则其体积为________.解析:该几何体是底面圆半经为 1,高为 2 的圆锥体的一半,故所求体积为 V=××(π×12)×2=.答案:5.(2013·辽宁高考)某几何体的三视图如图所示,则该几何体的体积是________.解析:由三视图可知该几何体是一个底面半径为 2,高为 4 的圆柱中间挖去一个底面边长为 2,高为 4 的正四棱柱后剩下的部分,所以其体积为 π×22×4-22×4=16π-16.答案:16π-16 易误警示(九)对几何体的形状判断不准致误[典例] (2013·重庆高考)某几何体的三视图如图所示,则该几何体的体积为( ) A. B. C.200 D.240[解题指导] 将三视...