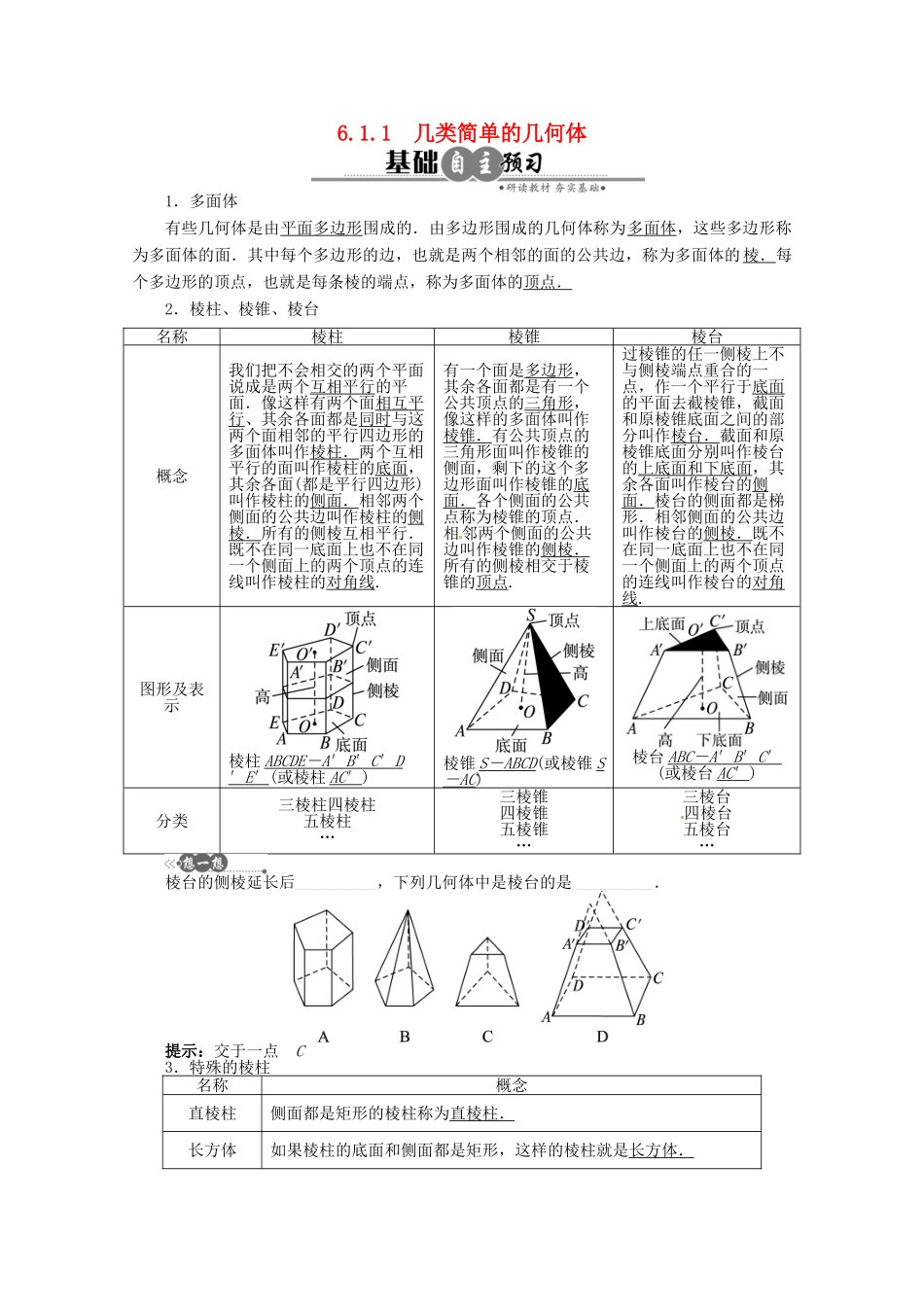
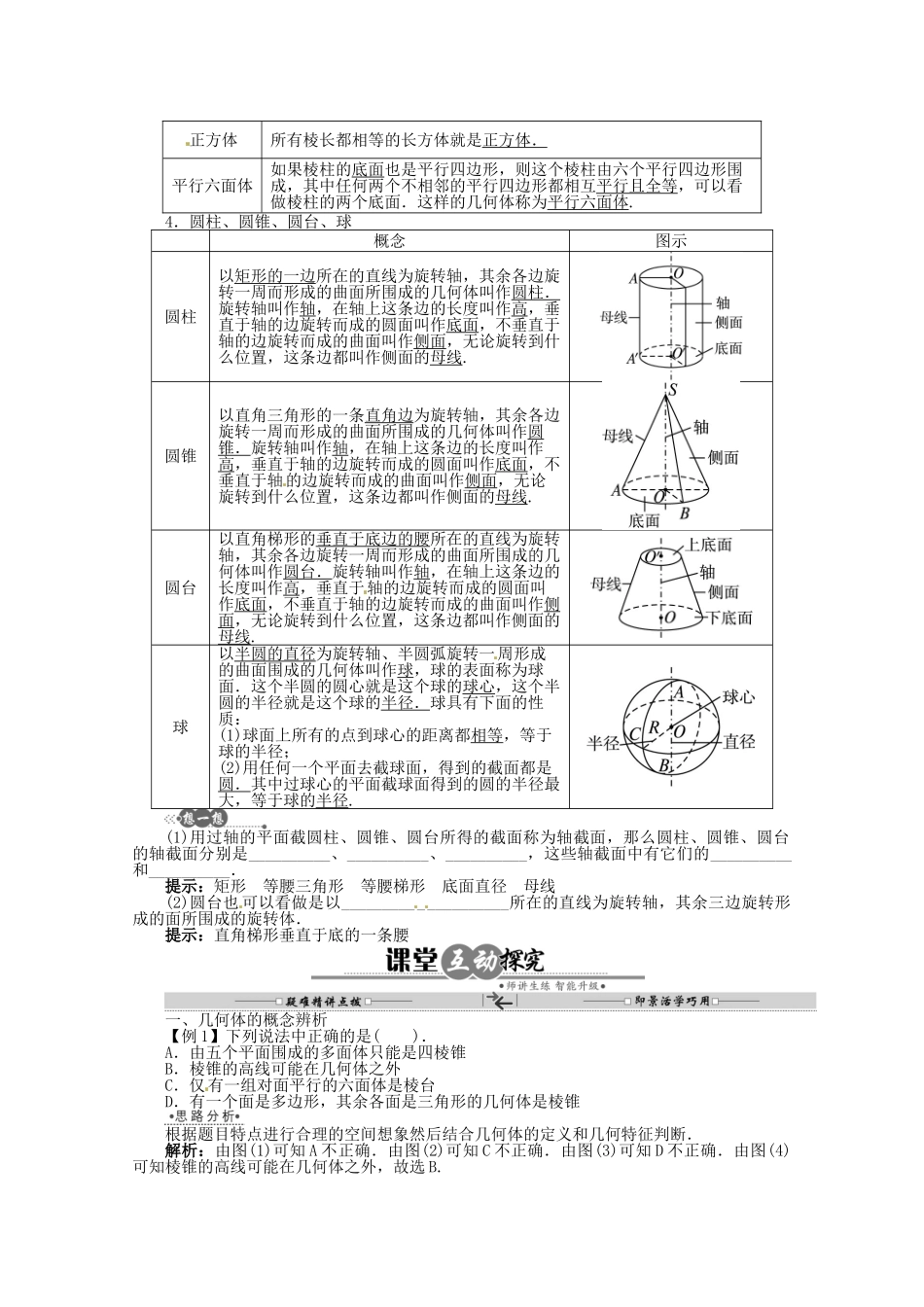
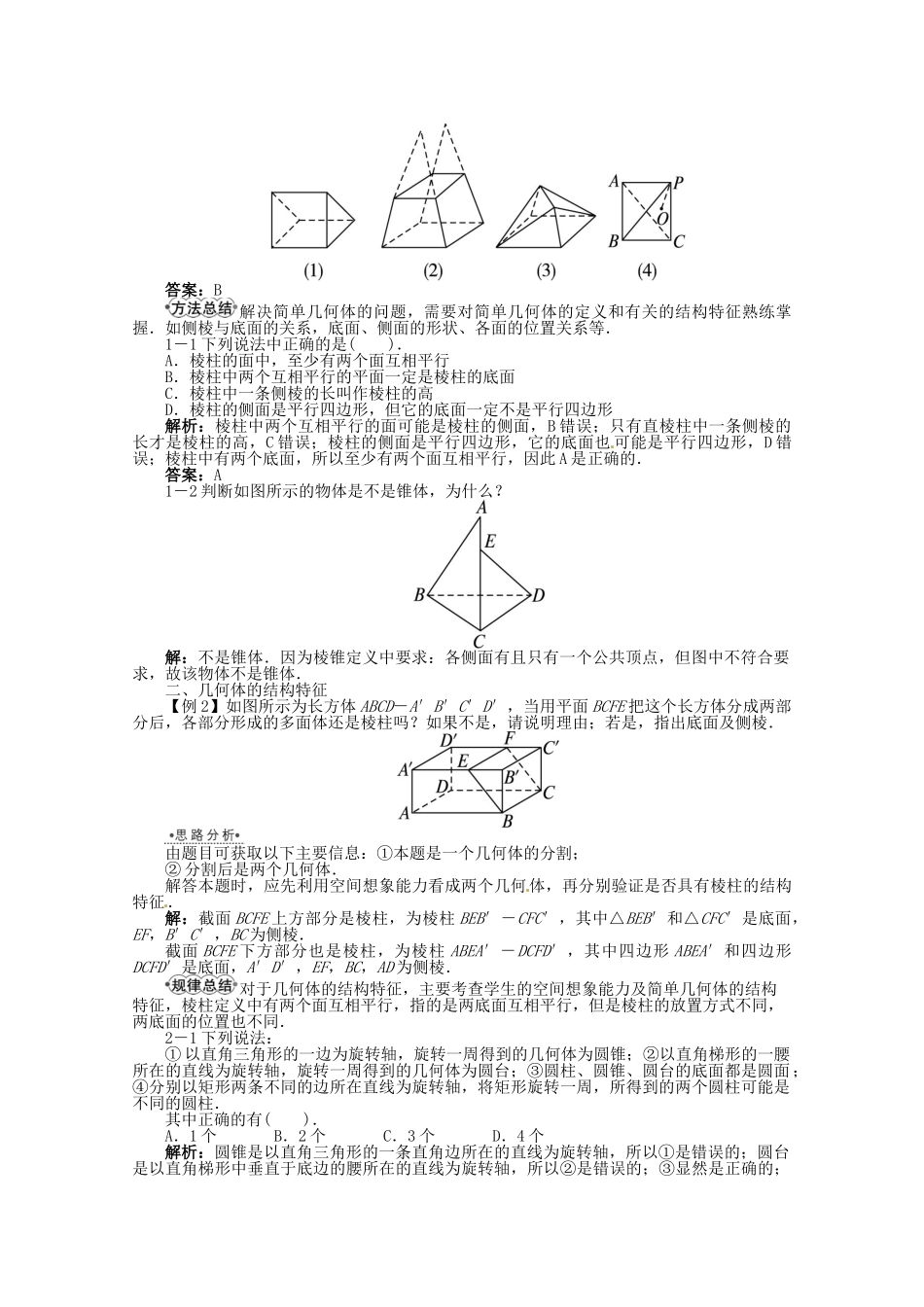
6.1.1 几类简单的几何体1.多面体有些几何体是由平面多边形围成的.由多边形围成的几何体称为多面体,这些多边形称为多面体的面.其中每个多边形的边,也就是两个相邻的面的公共边,称为多面体的棱.每个多边形的顶点,也就是每条棱的端点,称为多面体的顶点.2.棱柱、棱锥、棱台名称棱柱棱锥棱台概念我们把不会相交的两个平面说成是两个互相平行的平面.像这样有两个面相互平行、其余各面都是同时与这两个面相邻的平行四边形的多面体叫作棱柱.两个互相平行的面叫作棱柱的底面,其余各面(都是平行四边形)叫作棱柱的侧面.相邻两个侧面的公共边叫作棱柱的侧棱.所有的侧棱互相平行.既不在同一底面上也不在同一个侧面上的两个顶点的连线叫作棱柱的对角线.有一个面是多边形,其余各面都是有一个公共顶点的三角形,像这样的多面体叫作棱锥.有公共顶点的三角形面叫作棱锥的侧面,剩下的这个多边形面叫作棱锥的底面.各个侧面的公共点称为棱锥的顶点.相邻两个侧面的公共边叫作棱锥的侧棱.所有的侧棱相交于棱锥的顶点.过棱锥的任一侧棱上不与侧棱端点重合的一点,作一个平行于底面的平面去截棱锥,截面和原棱锥底面之间的部分叫作棱台.截面和原棱锥底面分别叫作棱台的上底面和下底面,其余各面叫作棱台的侧面.棱台的侧面都是梯形.相邻侧面的公共边叫作棱台的侧棱.既不在同一底面上也不在同一个侧面上的两个顶点的连线叫作棱台的对角线.图形及表示棱柱 ABCDE - A ′ B ′ C ′ D ′ E ′ (或棱柱 AC ′ )棱锥 S - ABCD (或棱锥 S- AC )棱台 ABC - A ′ B ′ C ′ (或棱台 AC ′ )分类三棱柱四棱柱五棱柱…三棱锥四棱锥五棱锥…三棱台四棱台五棱台…棱台的侧棱延长后__________,下列几何体中是棱台的是__________.提示:交于一点 C3.特殊的棱柱名称概念直棱柱侧面都是矩形的棱柱称为直棱柱.长方体如果棱柱的底面和侧面都是矩形,这样的棱柱就是长方体.正方体所有棱长都相等的长方体就是正方体.平行六面体如果棱柱的底面也是平行四边形,则这个棱柱由六个平行四边形围成,其中任何两个不相邻的平行四边形都相互平行且全等,可以看做棱柱的两个底面.这样的几何体称为平行六面体.4.圆柱、圆锥、圆台、球概念图示圆柱以矩形的一边所在的直线为旋转轴,其余各边旋转一周而形成的曲面所围成的几何体叫作圆柱.旋转轴叫作轴,在轴上这条边的长度叫作高,垂直于轴的边旋转而成的圆面叫作底面,不垂直于...