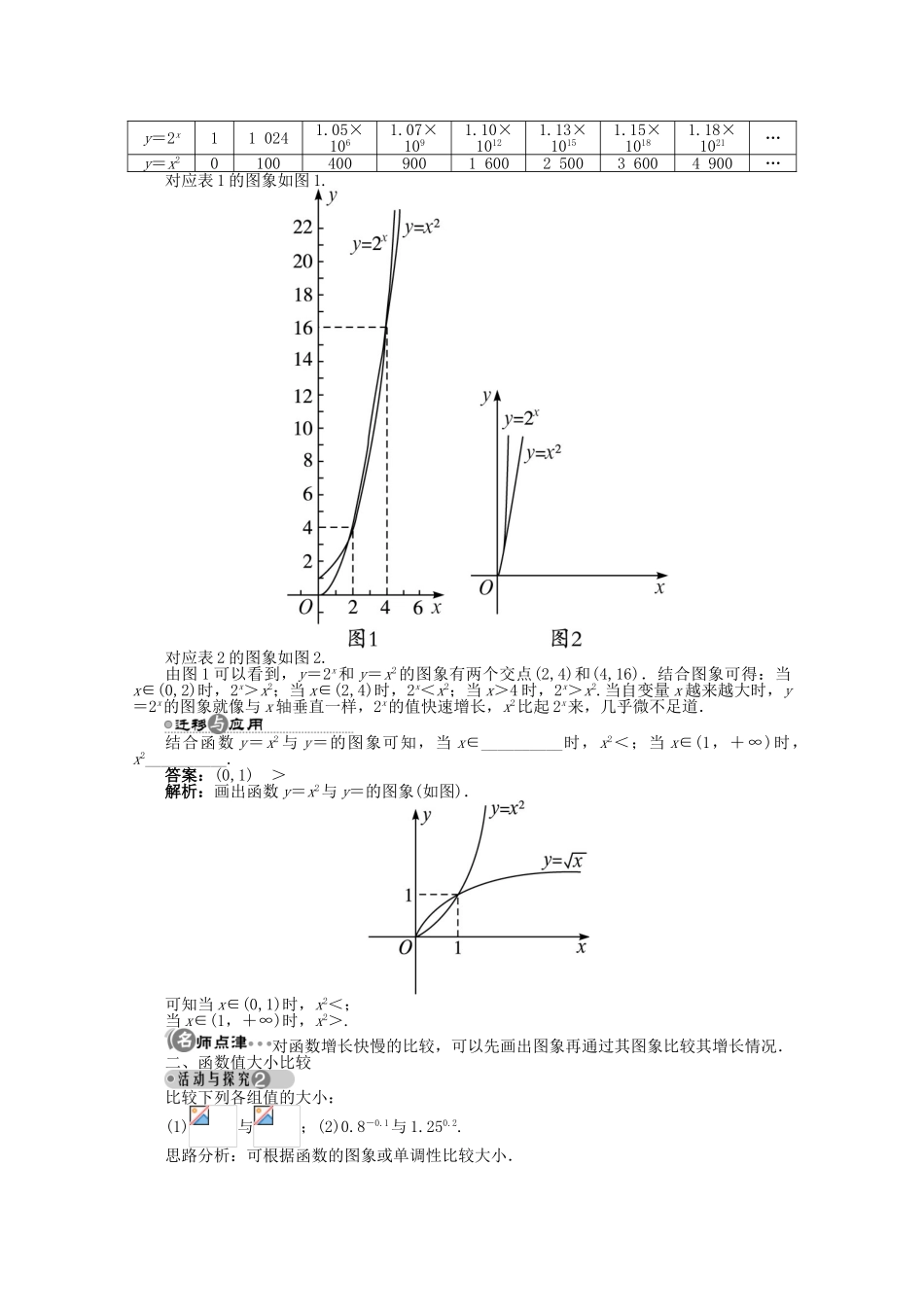
2.5.1 几种函数增长快慢的比较学习目标重点难点1.能知道不同的函数增长的速度有所不同;2.会分析不同函数的增长速度的快慢;3.记住常见的指数函数、对数函数、幂函数、一次函数的增长速度的不同.重点:常见函数如指数函数、对数函数、幂函数、一次函数增长速度的比较;难点:函数增长速度的比较.1.三种函数模型的性质2.三种函数的增长速度比较(1)在区间(0,+∞)上,函数 y=ax(a>1),y=logax(a>1)和 y=xn(n>0)都是增函数,但增长速度不同,且不在同一个“档次”上.(2)在区间(0,+∞)上随着 x 的增大,y=ax(a>1)增长速度越来越快,会超过并远远大于 y=xn(n>0)的增长速度,而 y=logax(a>1)的增长速度则会越来越慢.(3)存在一个 x0,使得当 x>x0时,有 logax < x n < a x .预习交流 1对于指数函数 y=ax(a>1),底数 a 的大小怎样影响函数的增长速度?提示:底数 a 越大,函数增长得越快.预习交流 2对于对数函数 y=logax(a>1),底数 a 的大小怎样影响函数的增长速度?提示:底数 a 越小,函数增长得越快.预习交流 3对于幂函数 y=xα,其增长速度快慢与 α 的关系是怎样的?提示:对于幂函数 y=xα,当 α 越大时,其增长速度越大.预习交流 4对于一次函数 y=kx+b(k>0),其增长速度快慢与 k 的关系是怎样的?提示:k 越大,增长速度越快.预习交流 5就指数函数、对数函数、幂函数而言,哪种增长速度最快?哪种最慢?提示:指数函数的增长速度最快,对数函数的增长速度最慢,幂函数的增长速度介于指数函数和对数函数之间.一、函数增长快慢的比较试利用图象比较 y=x2(x≥0)和 y=2x(x≥0)的增长情况.思路分析:先利用列表、描点、连线法画出两个函数的图象,再通过图象比较增长情况.解:列表如下:表 1x0246810121416…y=2x1416642561 0244 09616 38465 536…y=x204163664100144196256…表 2x010203040506070…y=2x11 0241.05×1061.07×1091.10×10121.13×10151.15×10181.18×1021…y=x201004009001 6002 5003 6004 900…对应表 1 的图象如图 1.对应表 2 的图象如图 2.由图 1 可以看到,y=2x和 y=x2的图象有两个交点(2,4)和(4,16).结合图象可得:当x∈(0,2)时,2x>x2;当 x∈(2,4)时,2x<x2;当 x>4 时,2x>x2.当自变量 x 越来越大时,y=2x的图象就像与 x 轴垂直一样,2x的值快速增长,x2比起 2x来,几乎微不足道.结合函数...