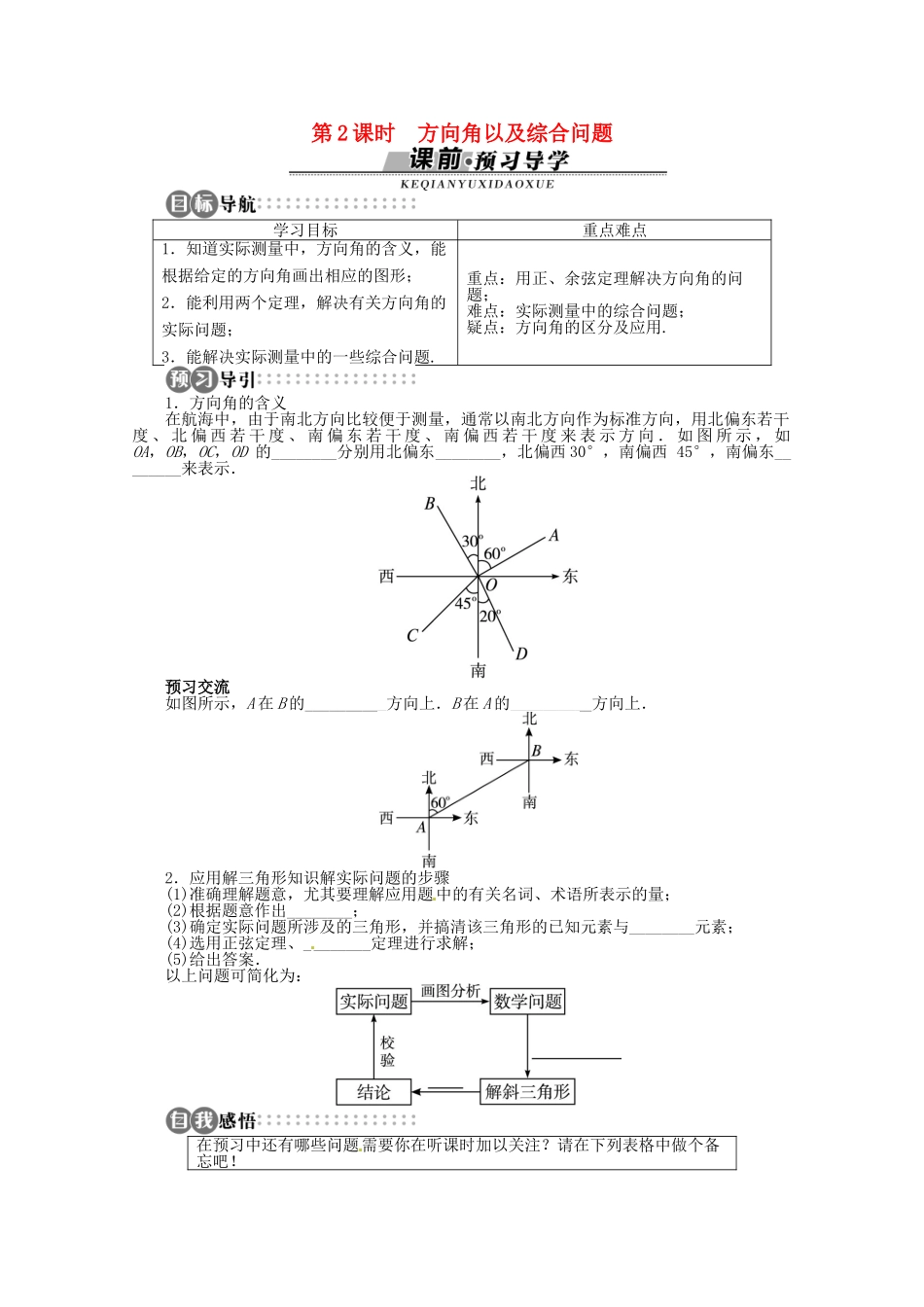
第 2 课时 方向角以及综合问题学习目标重点难点1.知道实际测量中,方向角的含义,能根据给定的方向角画出相应的图形;2.能利用两个定理,解决有关方向角的实际问题;3.能解决实际测量中的一些综合问题.重点:用正、余弦定理解决方向角的问题;难点:实际测量中的综合问题;疑点:方向角的区分及应用.1.方向角的含义在航海中,由于南北方向比较便于测量,通常以南北方向作为标准方向,用北偏东若干度 、 北 偏 西 若 干 度 、 南 偏 东 若 干 度 、 南 偏 西 若 干 度 来 表 示 方 向 . 如 图 所 示 , 如OA,OB,OC,OD 的________分别用北偏东________,北偏西 30°,南偏西 45°,南偏东________来表示.预习交流如图所示,A 在 B 的__________方向上.B 在 A 的__________方向上.2.应用解三角形知识解实际问题的步骤(1)准确理解题意,尤其要理解应用题中的有关名词、术语所表示的量;(2)根据题意作出________;(3)确定实际问题所涉及的三角形,并搞清该三角形的已知元素与________元素;(4)选用正弦定理、________定理进行求解;(5)给出答案.以上问题可简化为:在预习中还有哪些问题需要你在听课时加以关注?请在下列表格中做个备忘吧!我的学困点我的学疑点答案:1.方向角 60° 20°预习交流 1:提示:南偏西 60° 北偏东 60°2.(2)示意图 (3)未知 (4)余弦 (5)正、余弦定理 转化一、方向角问题某海轮以 30 n mile/h 的速度航行,在 A 点测得海面上油井 P 在南偏东 60°方向,向北航行 40 min 后到达 B 点,测得油井 P 在南偏东 30°方向,海轮改为北偏东 60°的航向再行驶 80 min 到达 C 点,求 P,C 间的距离.思路分析:先在△APB 中,利用正弦定理求出 BP 的长度,而 BC 的长度可求,∠CBP 的大小也可求,故在△PBC 中由余弦定理可求出 P,C 间的距离.如图,一艘船以 32.2 n mile/h 的速度向正北方向航行.在 A 处看灯塔 S 在船的北偏东20°的方向,30 min 后航行到 B 处,在 B 处看灯塔在船的北偏东 65°的方向,已知距离此灯塔 6.5 n mile 以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?解决方向角问题的关键是依据题意,画出恰当的示意图,将问题转化为三角形中的边和角问题,从而可利用正弦定理和余弦定理进行求解.二、综合应用问题在海岸 A 处,发现北偏东 45°方向,距离 A(-1) n mi...