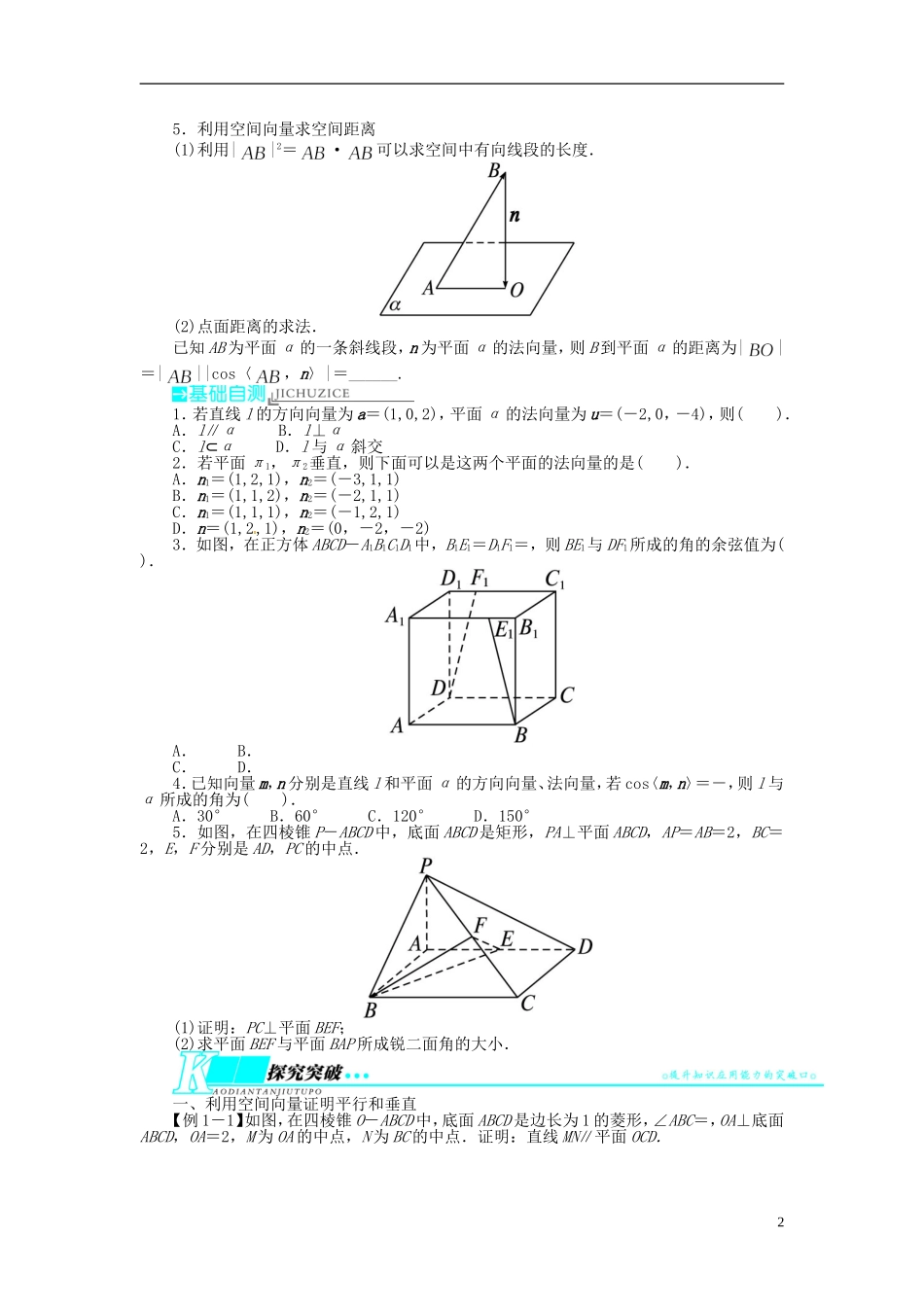
8.7 空间向量的应用考纲要求1.理解直线的方向向量与平面的法向量.2.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直、平行关系.3.能用向量方法证明有关直线和平面位置关系的一些定理(包括三垂线定理).4.能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题,了解向量方法在研究立体几何问题中的应用.1.直线的方向向量及其应用(1)直线的方向向量:直线的方向向量就是指和这条直线所对应向量____(或共线)的向量,显然一条直线的方向向量有____个.(2)直线方向向量的应用:利用直线的方向向量,可以确定空间中的直线和平面.① 对于直线 l,点 A 是直线 l 上一点,向量 a 是 l 的方向向量,在直线 l 上取=a,则对于直线 l 上任意一点 P,一定存在实数 t,使得______________.这样,点 A 和向量 a 不仅可以确定直线 l 的位置,还可以具体表示出 l 上的任意一点.② 空间中平面 α 的位置可以由 α 内两条相交直线确定,若设这两条直线相交于点 O,它们的方向向量分别是 a 和 b,P 为平面 α 上任意一点,由平面向量基本定理可知,存在有序实数对(x,y),使得=________,这样,点 O 与方向向量 a,b 不仅可以确定平面 α 的位置,还可以具体表示出 α 内的任意一点.2.平面的法向量(1)若直线 l⊥α,取直线 l 的方向向量 a,则向量 a 叫做平面 α 的法向量,显然一个平面的法向量也有____个,它们是____向量.(2)在空间中,给定一个点 A 和一个向量 a,那么,过点 A,以向量 a 为法向量的平面是____确定的.3.直线的方向向量与平面的法向量在确定直线、平面位置关系中的应用直线 l1的方向向量 u1=(a1,b1,c1),直线 l2的方向向量为 u2=(a2,b2,c2).(注:下面的λ,k∈R).如果 l1∥l2,那么 u1∥u2⇔u1=λu2⇔____________;如果 l1⊥l2,那么 u1⊥u2⇔u1·u2=0⇔____________.直线 l 的方向向量为 u=(a1,b1,c1),平面 α 的法向量为 n=(a2,b2,c2).若 l∥α,则 u⊥n⇔u·n=0⇔____________;若 l⊥α,则 u∥n⇔u=kn⇔________________.平面 α1的法向量为 u1=(a1,b1,c1),平面 α2的法向量为 u2=(a2,b2,c2).若 α1∥α2,则 u1∥u2⇔u1=ku2⇔______________;若 α1⊥α2,则 u1⊥u2⇔u1·u2=0⇔______________.4.利用空间向量求空间角(1)两条异面直线所成的角:① 范围:两异面直线所...