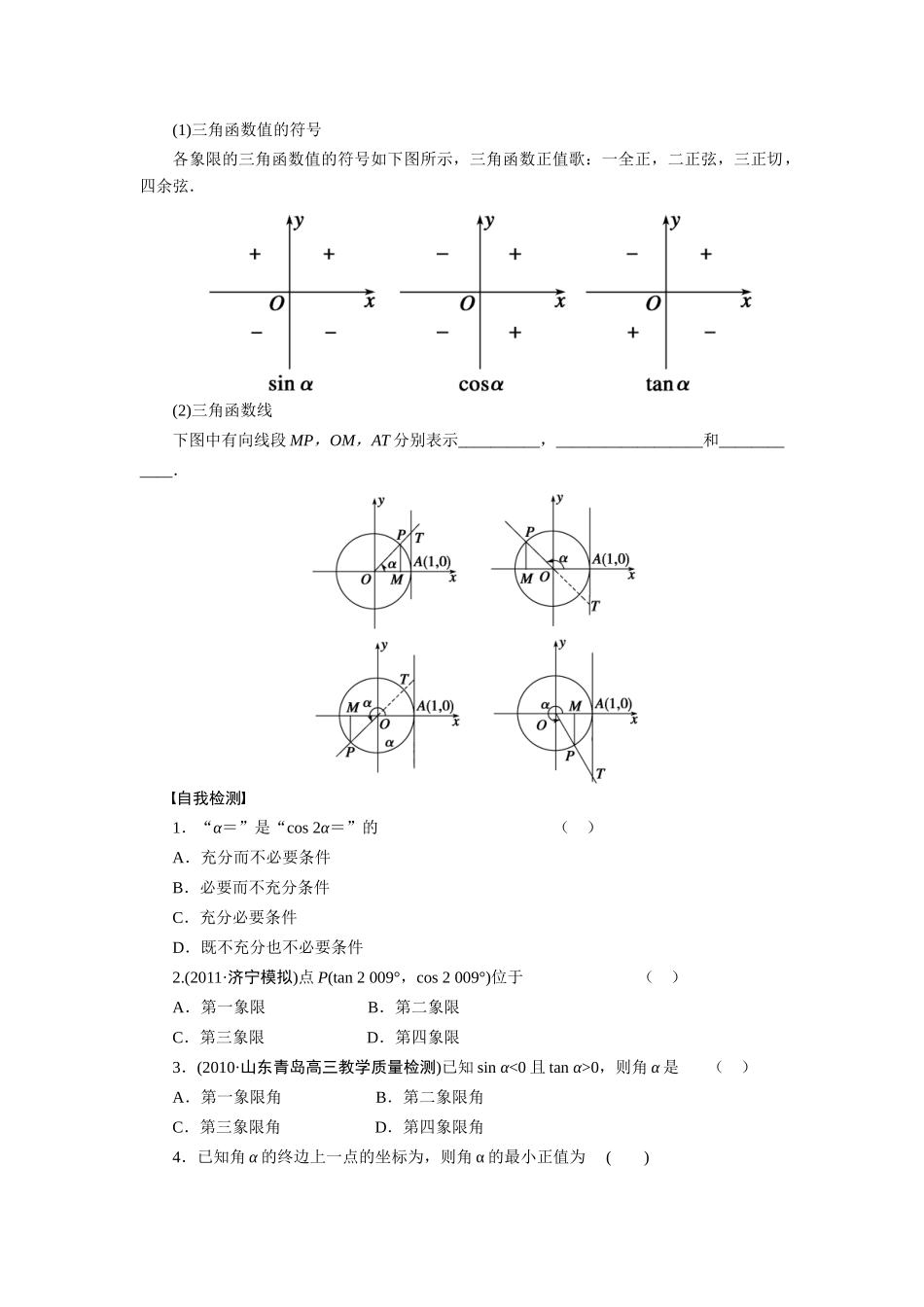
第四章 三角函数与三角恒等变换学案 17 任意角的三角函数导学目标: 1.了解任意角的概念.2.了解弧度制的概念,能进行弧度与角度的互化.3.理解任意角的三角函数(正弦、余弦、正切)的定义.自主梳理1.任意角的概念角可以看成平面内一条射线 OA 绕着端点从一个位置旋转到另一个位置 OB 所成的图形.旋转开始时的射线 OA 叫做角的________,射线的端点 O 叫做角的________,旋转终止位置的射线 OB 叫做角的________,按______时针方向旋转所形成的角叫做正角,按______时针方向旋转所形成的角叫做负角.若一条射线没作任何旋转,称它形成了一个________角.(1)象限角使角的顶点与原点重合,角的始边与 x 轴的非负半轴重合,角的终边落在第几象限,就说这个角是__________角.(2)象限界角(即终边在坐标轴上的角)终边在 x 轴上的角表示为____________________;终边在 y 轴上的角表示为__________________________________________;终边落在坐标轴上的角可表示为____________________________.(3)终边相同的角所有与角 α 终边相同的角,连同角 α 在内,可构成一个集合______________________或__________________________,前者 α 用角度制表示,后者 α 用弧度制表示.(4)弧度制把长度等于________长的弧所对的__________叫 1 弧度的角.以弧度作为单位来度量角的单位制,叫做________,它的单位符号是________,读作________,通常略去不写.(5)度与弧度的换算关系360°=______ rad;180°=____ rad;1°=________ rad;1 rad=_______________≈57.30°.(6)弧长公式与扇形面积公式l=________,即弧长等于_________________________________________________.S 扇=________=____________.2.三角函数的定义任意角的三角函数定义:设 α 是一个任意角,它的终边与单位圆交于点 P(x,y),那么①____叫做 α 的正弦,记作 sin α,即 sin α=y;②____叫做 α 的余弦,记作 cos α,即 cos α=x;③________叫做 α 的正切,记作 tan α,即 tan α= (x≠0).(1)三角函数值的符号各象限的三角函数值的符号如下图所示,三角函数正值歌:一全正,二正弦,三正切,四余弦.(2)三角函数线下图中有向线段 MP,OM,AT 分别表示__________,__________________和____________.自我检测1.“α=”是“cos 2α=”的 ( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件...