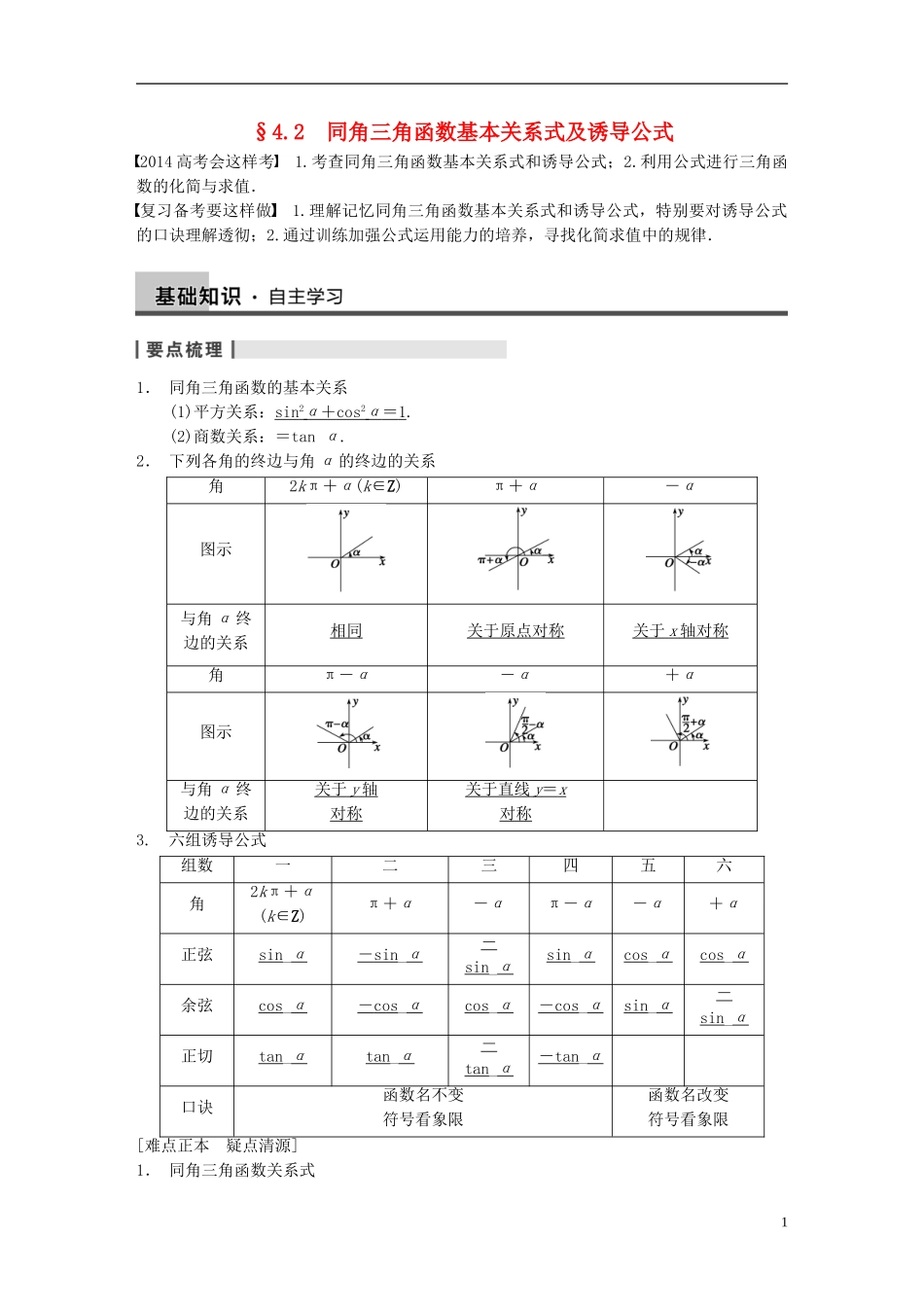
§4.2 同角三角函数基本关系式及诱导公式2014 高考会这样考 1.考查同角三角函数基本关系式和诱导公式;2.利用公式进行三角函数的化简与求值.复习备考要这样做 1.理解记忆同角三角函数基本关系式和诱导公式,特别要对诱导公式的口诀理解透彻;2.通过训练加强公式运用能力的培养,寻找化简求值中的规律.1. 同角三角函数的基本关系(1)平方关系:sin 2 α + cos 2 α = 1 .(2)商数关系:=tan α.2. 下列各角的终边与角 α 的终边的关系角2kπ+α(k∈Z)π+α-α图示与角 α 终边的关系相同关于原点对称关于 x 轴对称 角π-α-α+α图示与角 α 终边的关系关于 y 轴 对称关于直线 y = x 对称3. 六组诱导公式组数一二三四五六角2kπ+α(k∈Z)π+α-απ-α-α+α正弦sin_α- sin _α-sin_αsin_αcos_αcos_α余弦cos_α- cos _αcos_α- cos _αsin_α-sin_α正切tan_αtan_α-tan_α- tan _α口诀函数名不变符号看象限函数名改变符号看象限[难点正本 疑点清源]1. 同角三角函数关系式1(1)利用平方关系解决问题时,要注意开方运算结果的符号,需要根据角 α 的范围进行确定.(2)同角三角函数的基本关系反映了同一个角的不同三角函数之间的必然联系,它为三角函数的化简、求值、证明等又提供了一种重要的方法.2. 诱导公式诱导公式可概括为 k·±α(k∈Z)的各三角函数值的化简公式.记忆规律是“奇变偶不变,符号看象限”.其中的奇、偶是指的奇数倍和偶数倍,变与不变是指函数名称的变化.1. (2011·大纲全国)已知 α∈,tan α=2,则 cos α=________.答案 -解析 tan α=2,∴=2,∴sin α=2cos α.又 sin2α+cos2α=1,∴(2cos α)2+cos2α=1,∴cos2α=.又 α∈,∴cos α=-.2. 若 tan α=2,则的值为________.答案 解析 原式==.3. 已知 α 是第二象限的角,tan α=-,则 cos α=________.答案 -解析 α 是第二象限的角,∴cos α<0.又 sin2α+cos2α=1,tan α==-,∴cos α=-.4. sin π·cos π·tan 的值是________.答案 -解析 原式=sin·cos·tan=··=××(-)=-.5. 已知 cos=,则 sin=________.答案 -解析 sin=sin=-sin=-cos=-.题型一 同角三角函数基本关系式的应用例 1 已知在△ABC 中,sin A+cos A=.(1)求 sin Acos A 的值;(2)判断△ABC 是锐...