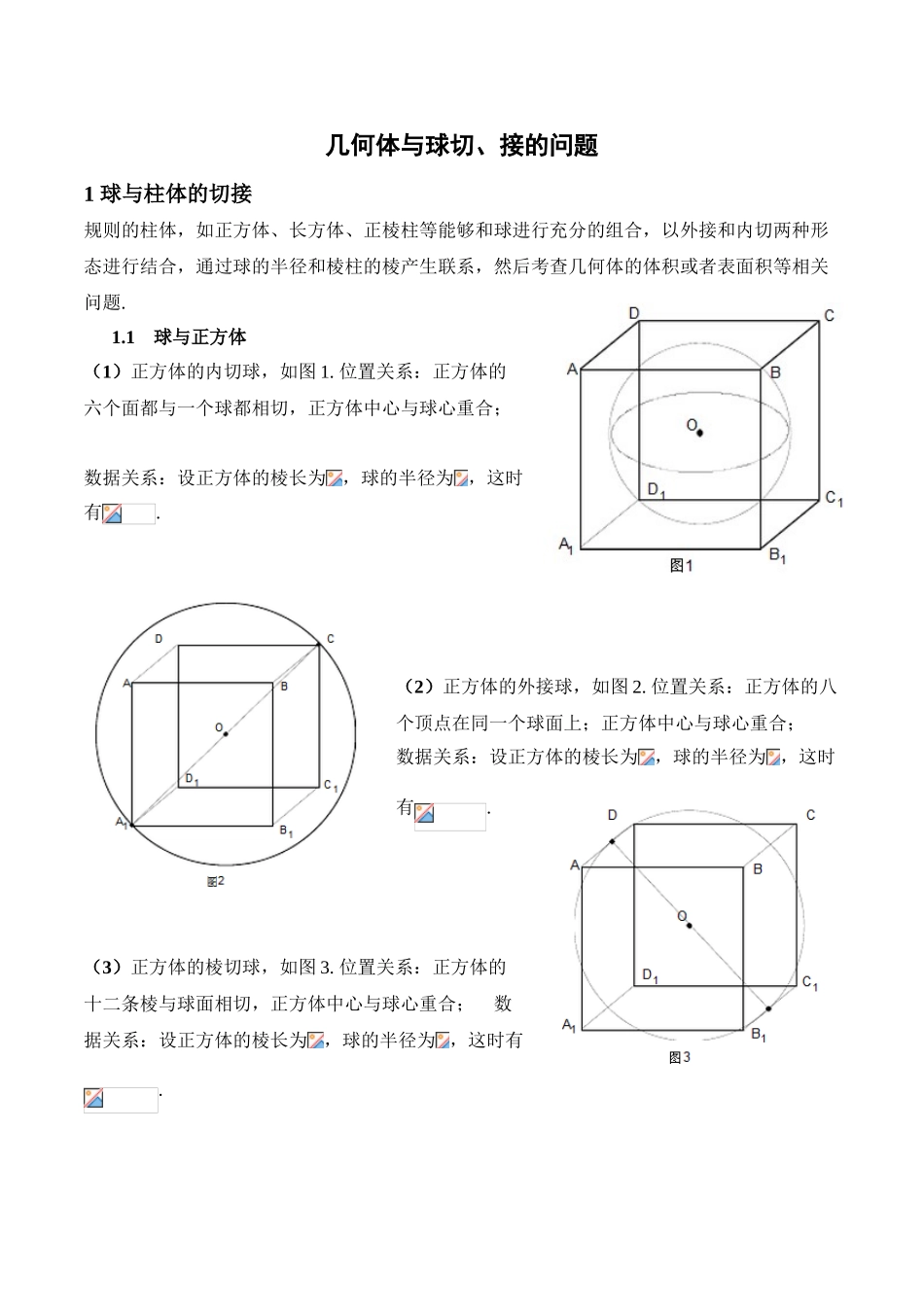
几何体与球切、接的问题1 球与柱体的切接规则的柱体,如正方体、长方体、正棱柱等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱柱的棱产生联系,然后考查几何体的体积或者表面积等相关问题.1.1 球与正方体(1)正方体的内切球,如图 1. 位置关系:正方体的六个面都与一个球都相切,正方体中心与球心重合; 数据关系:设正方体的棱长为,球的半径为 ,这时有. (2)正方体的外接球,如图 2. 位置关系:正方体的八个顶点在同一个球面上;正方体中心与球心重合; 数据关系:设正方体的棱长为,球的半径为 ,这时有.(3)正方体的棱切球,如图 3. 位置关系:正方体的十二条棱与球面相切,正方体中心与球心重合; 数据关系:设正方体的棱长为,球的半径为 ,这时有.1、 棱长为 1 的正方体内有一个球与正方体的 12 条棱都相切,则球的体积为( ) A.4π B. C. D.π1.2 球与长方体2、已知各顶点都在一个球面上的正四棱柱高为 4,体积为 16,则这个球的表面积为( ).A. B. C. D.1.3 球与直柱体3、一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的高为,底面周长为 3,那么这个球的体积为 _________ .2 球与锥体的切接规则的锥体,如正四面体、正棱锥、特别的一些棱锥等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱锥的棱和高产生联系,然后考查几何体的体积或者表面积等相关问题.2.1 正四面体与球的切接问题 (1) 正四面体的内切球,如图 4. 位置关系:正四面体的四个面都与一个球相切,正四面体的中心与球心重合; 数据关系:设正四面体的棱长为,高为;球的半径为,这时有; (2) 正四面体的外接球,如图 5. 位置关系:正四面体的四个顶点都在一个球面上,正四面体的中心与球心重合; 数据关系:设正四面体的棱长为,高为;球的半径为,这时有; (3) 正四面体的棱切球,如图 6. 位置关系:正四面体的六条棱与球面相切,正四面体的中心与球心重合; 数据关系:设正四面体的棱长为,高为;球的半径为,这时有 4、设正四面体中,第一个球是它的内切球,第二个球是它的外接球,求这两个球的表面积之比及体积之比.2.2 直角三棱锥5、自半径为的球面上一点,引球的三条两两垂直的弦,求的值.6、若三棱锥的三条侧棱两两垂直,且侧棱长均为,则其外接球的表面积是.7、在三棱椎 ABCD...