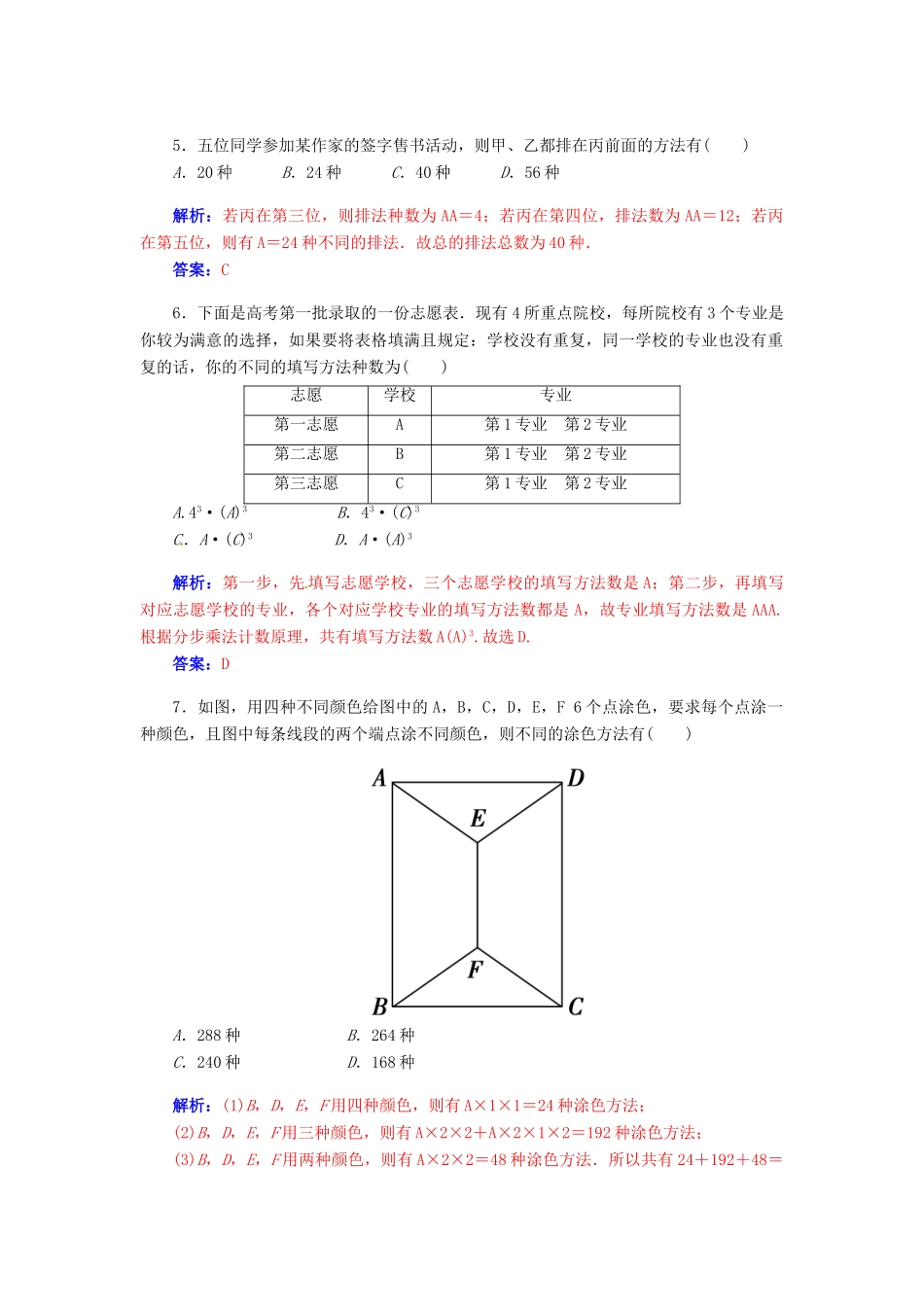
第二节 排列与组合(一)1.(2013·威海模拟)将 a,b,c 三个字母填写到 3×3 方格中,要求每行每列都不能出现重复字母,不同的填写方法有( )A.9 B.10 C.12 D.16 解析:先填 第一行,则第一行有 A=6 种,第二行第一列有 2 种,其余 2 列有唯一 1 种,第三列唯一确定 1 种,共有 6×2=12(种).答案:C2.用 0,1,2,3,4 排成无重复数字的五位数,要求偶数字相邻,奇数字也相邻,则这样的五位数的个数是( )A.36 B.32 C.24 D.20解析:将 3 个偶数“捆绑”,2 个奇数“捆绑”,这样得到 2 个新元素,将这 2 个新元素排列,得到种数为 AAA,其中,0 在首位的有四个:02 413,02 431,04 213,04 231,所以,这样的五位数的个数是 AAA-4=20.故选 D.答案:D3.有 5 盆菊花,其中黄菊花 2 盆、白菊花 2 盆、红菊花 1 盆,现把它们摆放成一排,要求 2 盆黄菊花必须相邻,2 盆白菊花不能相邻,则这 5 盆花的不同摆放种数是( )A.12 B.24 C.36 D.48解析:利用相邻问题捆绑法,间隔问题插空法得:AAA=24,故选 B.答案:B4.如图,一环形花坛分成 A,B,C,D 4 块,现有 4 种不同的花供选种,要求在每块里种 1 种花,且相邻的 2 块种不同的花,则不同的种法总数为( ) A.96 B.84 C.60 D.48解析:分三类:种 2 种花有 A 种种法;种 3 种花有 2A 种种法;种 4 种花有 A 种种法.所以共有 A+2A+A=84 种.故选 B.另解:按 A-B-C-D 顺序种花,可分 A,C 同色与不同色有 4×3×(1×3+2×2)=84种.故选 B.答案:B5.五位同学参加某作家的签字售书活动,则甲、乙都排在丙前面的方法有( )A.20 种 B.24 种 C.40 种 D.56 种解析:若丙在第三位,则排法种数为 AA=4;若丙在第四位,排法数为 AA=12;若丙在第五位,则有 A=24 种不同的排法.故总的排法总数为 40 种.答案:C6.下面是高考第一批录取的一份志愿表.现有 4 所重点院校,每所院校有 3 个专业是你较为满意的选择,如果要将表格填满且规定:学校没有重复,同一学校的专业也没有重复的话,你的不同的填写方法种数为( )志愿学校专业第一志愿A第 1 专业 第 2 专业第二志愿B第 1 专业 第 2 专业第三志愿C第 1 专业 第 2 专业A.43·(A)3 B.43·(C)3C.A·(C)3 D.A·(A)3解析:第一步,先 填写志愿学校,三个志愿学校的填写方法数是 A;第二步,...