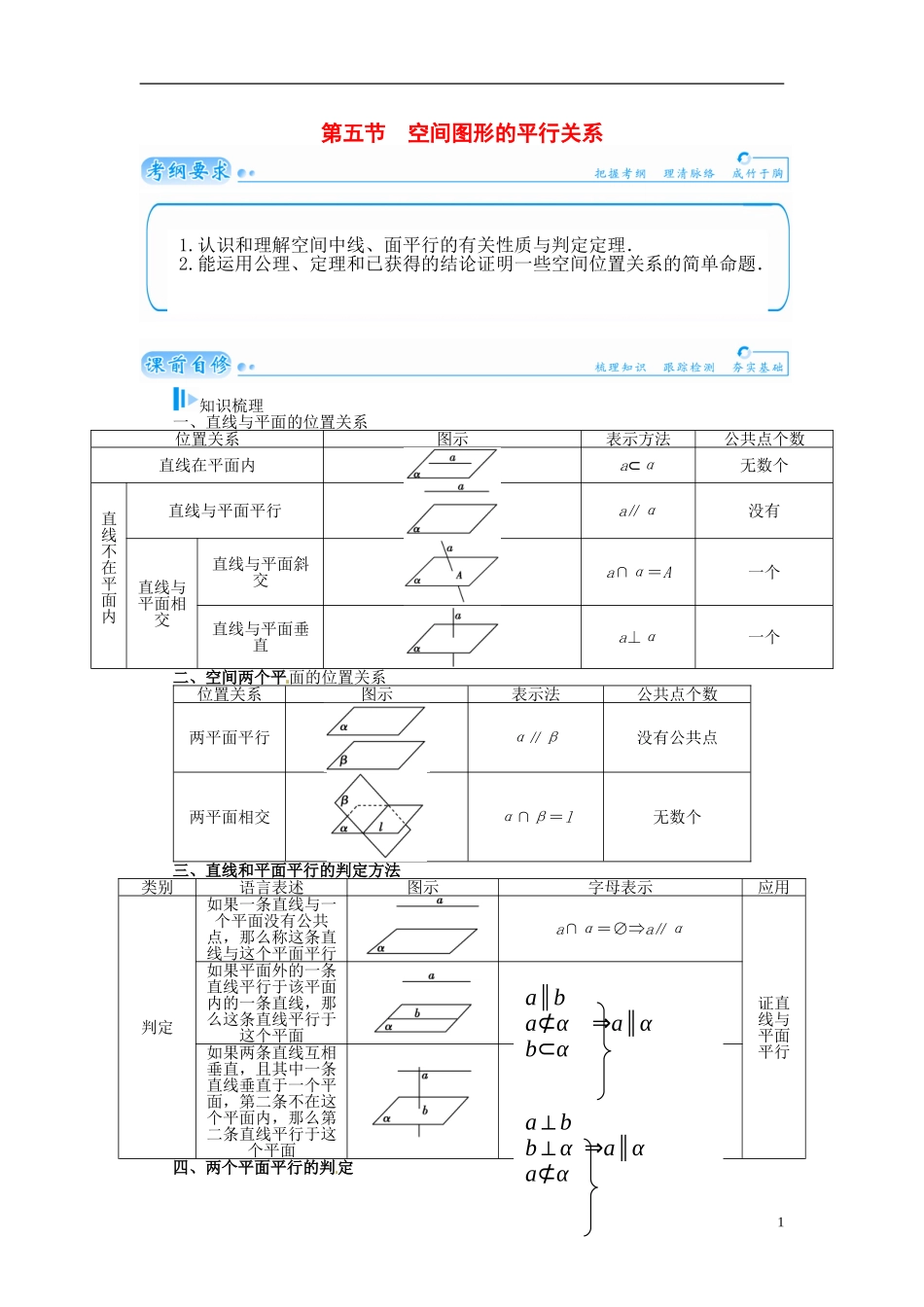
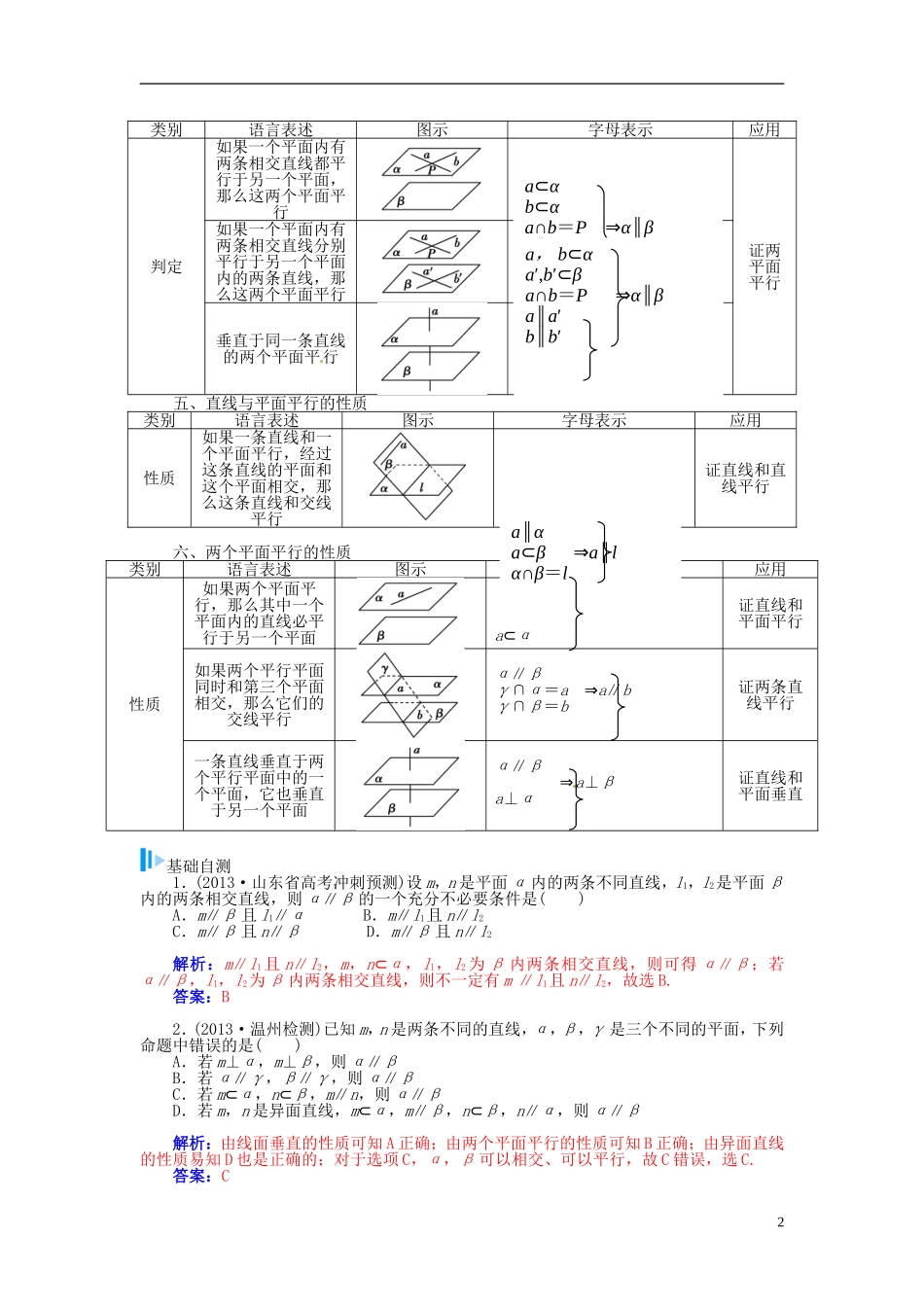
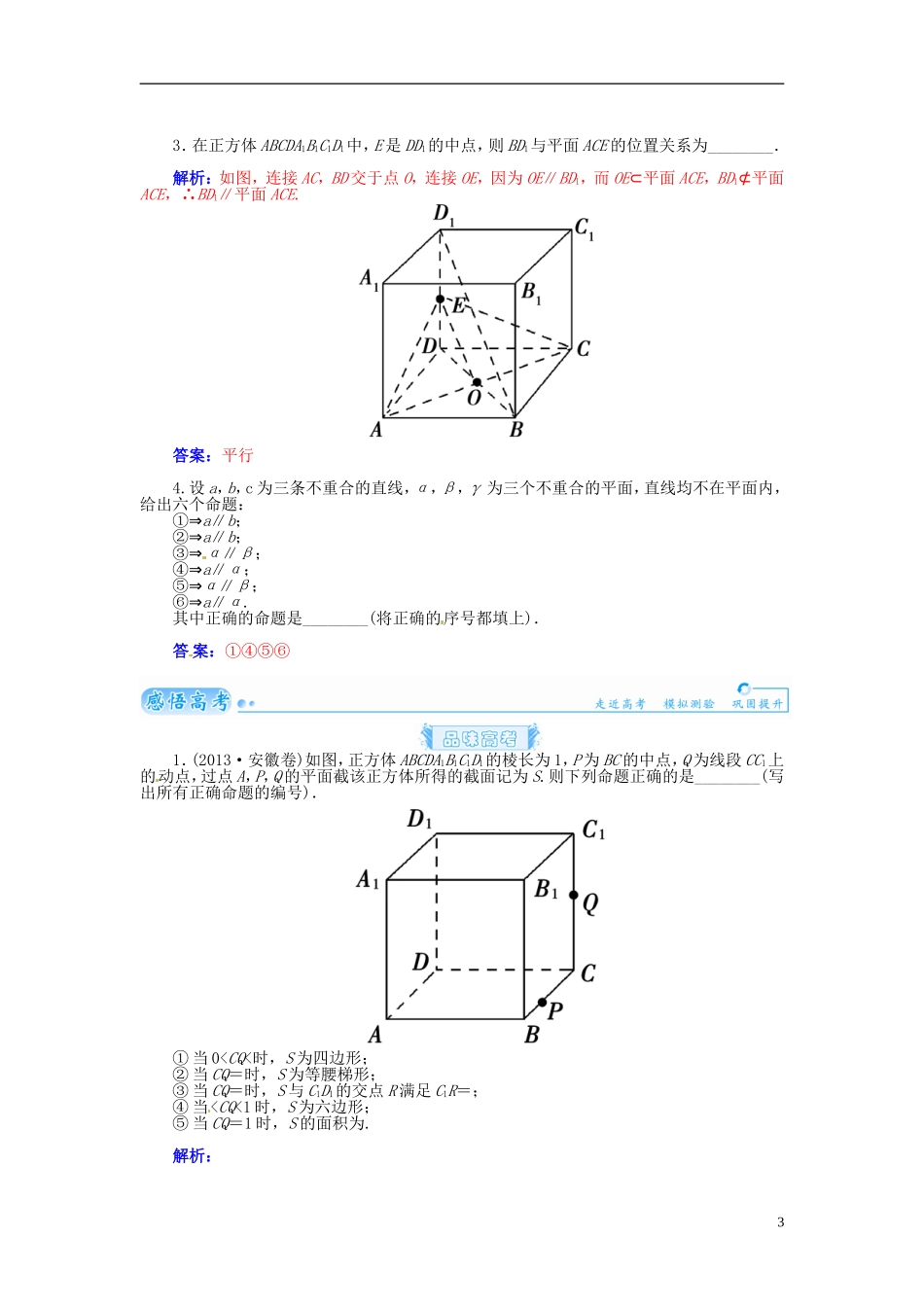
第五节 空间图形的平行关系知识梳理一、直线与平面的位置关系位置关系图示表示方法公共点个数直线在平面内a⊂α无数个直线不在平面内直线与平面平行a∥α没有直线与平面相交直线与平面斜交a∩α=A一个直线与平面垂直a⊥α一个二、空间两个平面的位置关系位置关系图示表示法公共点个数两平面平行α∥β没有公共点两平面相交α∩β=l无数个三、直线和平面平行的判定方法类别语言表述图示字母表示应用判定如果一条直线与一个平面没有公共点,那么称这条直线与这个平面平行a∩α=∅⇒a∥α证直线与平面平行如果平面外的一条直线平行于该平面内的一条直线,那么这条直线平行于这个平面如果两条直线互相垂直,且其中一条直线垂直于一个平面,第二条不在这个平面内,那么第二条直线平行于这个平面四、两个平面平行的判定11.认识和理解空间中线、面平行的有关性质与判定定理.2.能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题.a∥ba⊄α ⇒a∥αb⊂αa⊥bb⊥α ⇒a∥αa⊄α类别语言表述图示字母表示应用判定如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行证两平面平行如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行垂直于同一条直线的两个平面平行a⊥α⇒α∥β a⊥β五、直线与平面平行的性质类别语言表述图示字母表示应用性质如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行证直线和直线平行六、两个平面平行的性质类别语言表述图示字母表示应用性质如果两个平面平行,那么其中一个平面内的直线必平行于另一个平面α∥β ⇒a∥β a⊂α证直线和平面平行如果两个平行平面同时和第三个平面相交,那么它们的交线平行α∥βγ∩α=a ⇒a∥bγ∩β=b 证两条直线平行 一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面α∥β⇒a⊥β a⊥α证直线和平面垂直基础自测1.(2013·山东省高考冲刺预测)设 m,n 是平面 α 内的两条不同直线,l1,l2是平面 β内的两条相交直线,则 α∥β 的一个充分不必要条件是( )A.m∥β 且 l1∥α B.m∥l1且 n∥l2C.m∥β 且 n∥β D.m∥β 且 n∥l2解析:m∥l1 且 n∥l2,m,n⊂α,l1,l2 为 β 内两条相交直线,则可得 α∥β;若α∥β,l1,l2为 β 内两条相交直线,则不一定有 m ∥l1且 n∥l2,故选 B.答案:B2.(2013·温州检测)...