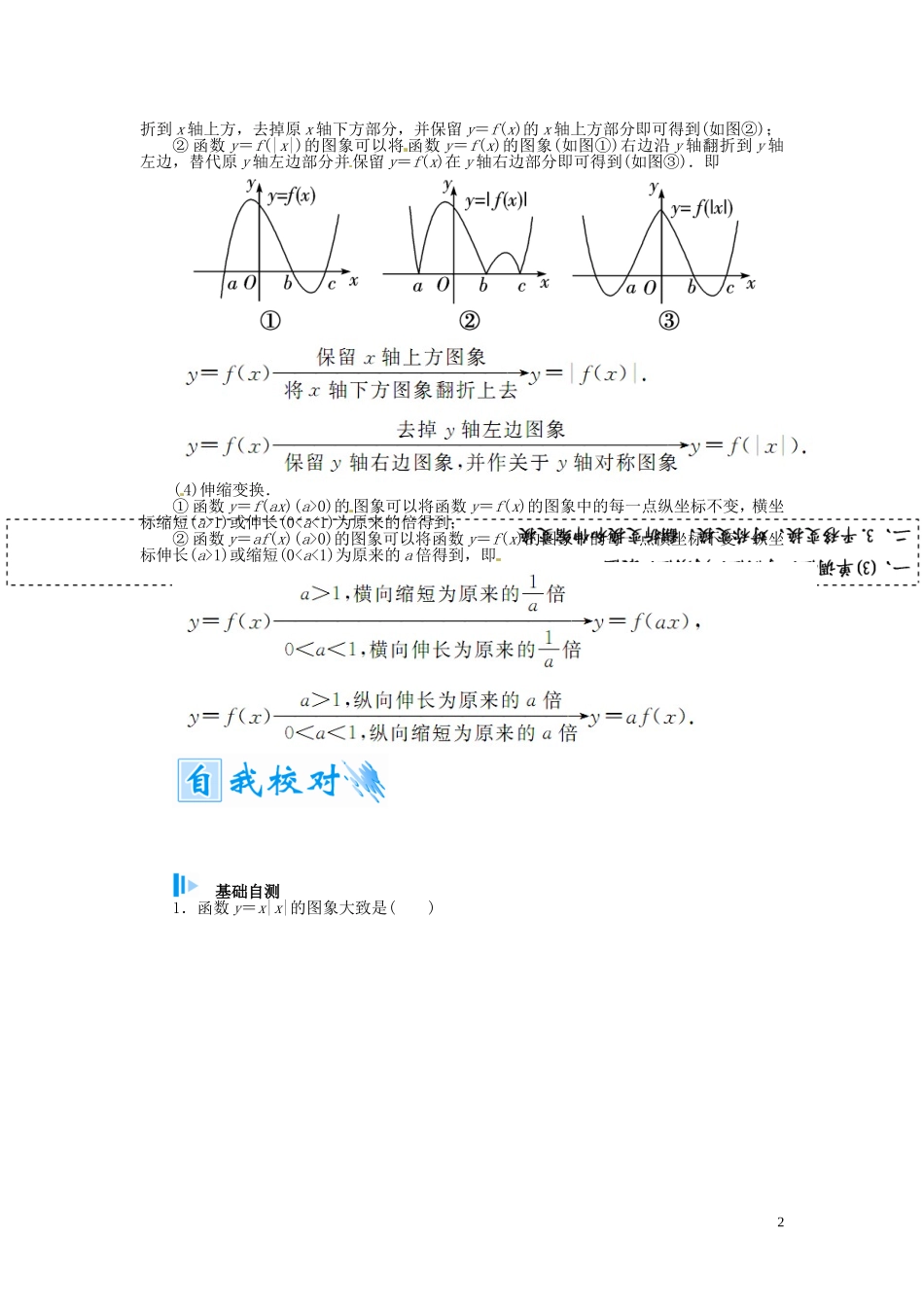
第九节 函数的图象及其变换 知识梳理 函数图象的作图方法有两种:描点法和利用基本函数图象变换作图. 一、描点法作图用描点法作函数图象的步骤:( 1)确定函数的定义域;(2)化简函数的解析式;(3)讨论函数的性质即___ _________(甚至变化趋势);(4)描点连线,画出函数的图象.二、图象变换法作图1.要准确记忆一次函数、二次函数、反比例函数、幂函数、指数函数、对数函数、三角函数等基本初等函数的图象及性质.2.识图:分布范围、变化 趋势、对称性、周期性等.3.四种图象变换:________________________.(1)平移变换.① 水平平移:函数 y=f(x+h)的图象可以把函数 y=f(x)的图象沿 x 轴方向向左(h>0)或向右(h<0)平移|h|个单位长度得到,即 y=f(x)――――――――→y=f(x+h);② 竖直平移:函数 y=f(x)+k 的图象可以把函数 y=f(x)的图象沿 y 轴方向向上(k>0)或向下(k<0)平移|k|个单位长度得到,即 y=f(x)―――――→y=f(x)+k.(2)对称变换.① 函数 y=-f(x)的图象可以将函数 y=f(x)的图象关于 x 轴对称得到;② 函数 y=f(-x)的图象可以将函数 y=f(x)的图象关于 y 轴对称得到;③ 函数 y=-f(-x)的图象可以将函数 y=f(x)的图象关于原点对称得到;④ 函数 y=f-1(x)的图象可以将函数 y=f(x)的图象关于直线 y=x 对称得到;(3)翻折变换.① 函数 y=|f(x)|的图象可以将函数 y=f(x)的图象(如图①)的 x 轴下方部分沿 x 轴翻11.掌握图象变换的规律,如平移变换、对称变换、翻折变换、伸缩变换等.2.会运用函数图象理解和研究函数的性质.折到 x 轴上方,去掉原 x 轴下方部分,并保留 y=f(x)的 x 轴上方部分即可得到(如图②);② 函数 y=f(|x|)的图象可以将 函数 y=f(x)的图象(如图①)右边沿 y 轴翻折到 y 轴左边,替代原 y 轴左边部分并保留 y=f(x)在 y 轴右边部分即可得到(如图③).即( 4)伸缩变换.① 函数 y=f(ax)(a>0)的 图象可以将函数 y=f(x)的图象中的每一点纵坐标不变,横坐标缩短(a>1)或伸长(0
0)的图象可以将函数 y=f(x)的图象中的每一点横坐标不变,纵坐标伸长(a>1)或缩短(0b),若 f(x)的图象如下图所示,则函...