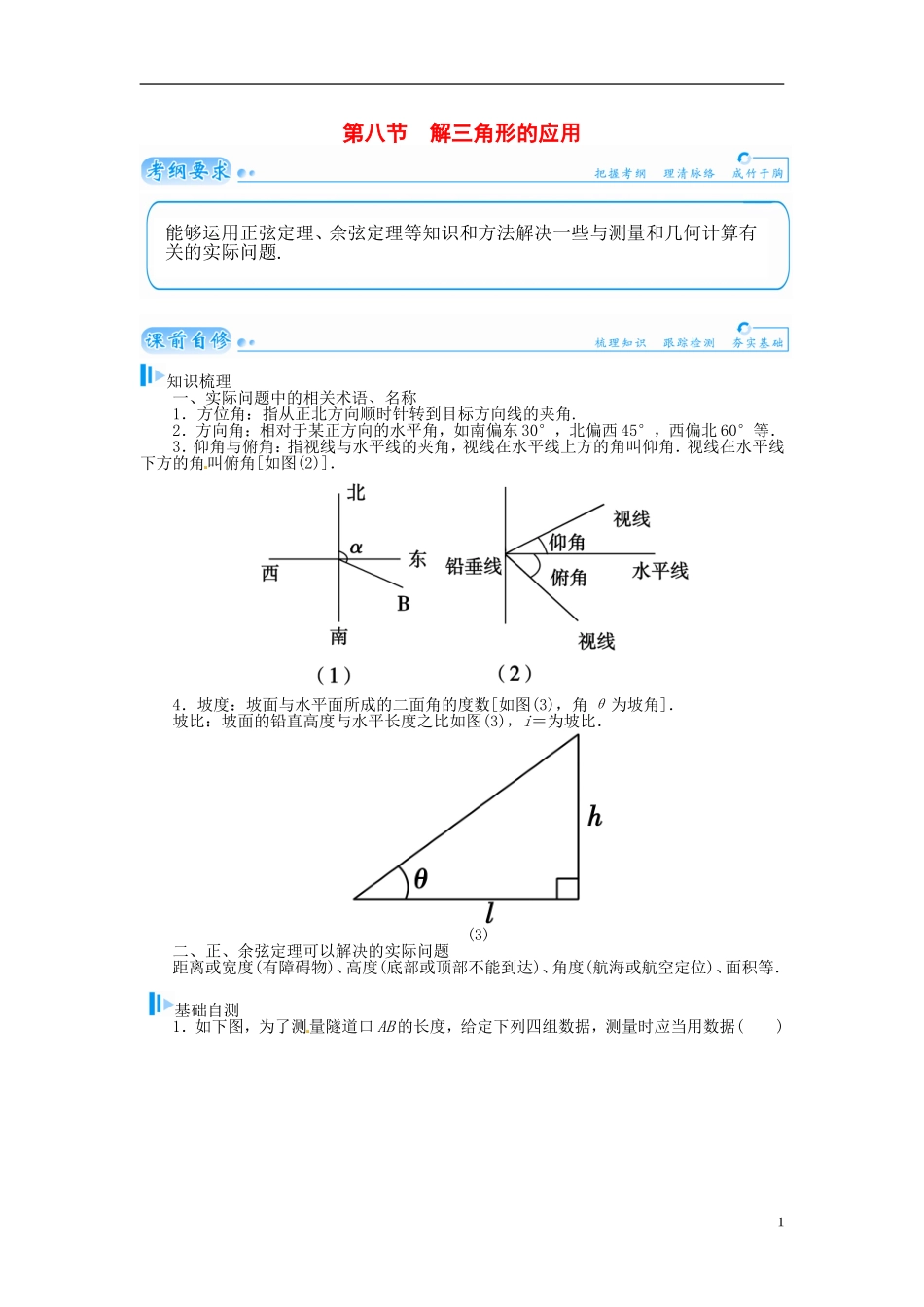
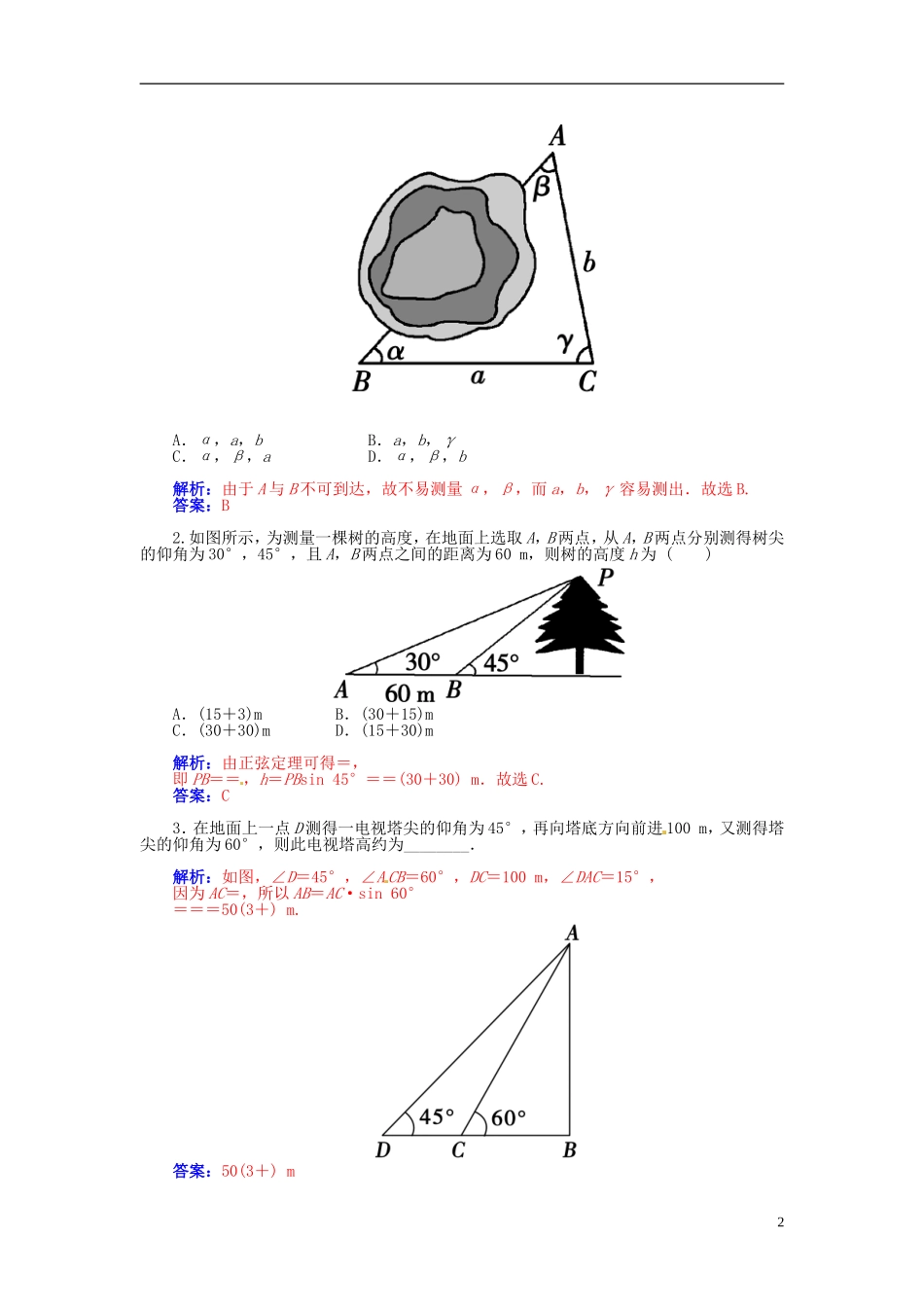
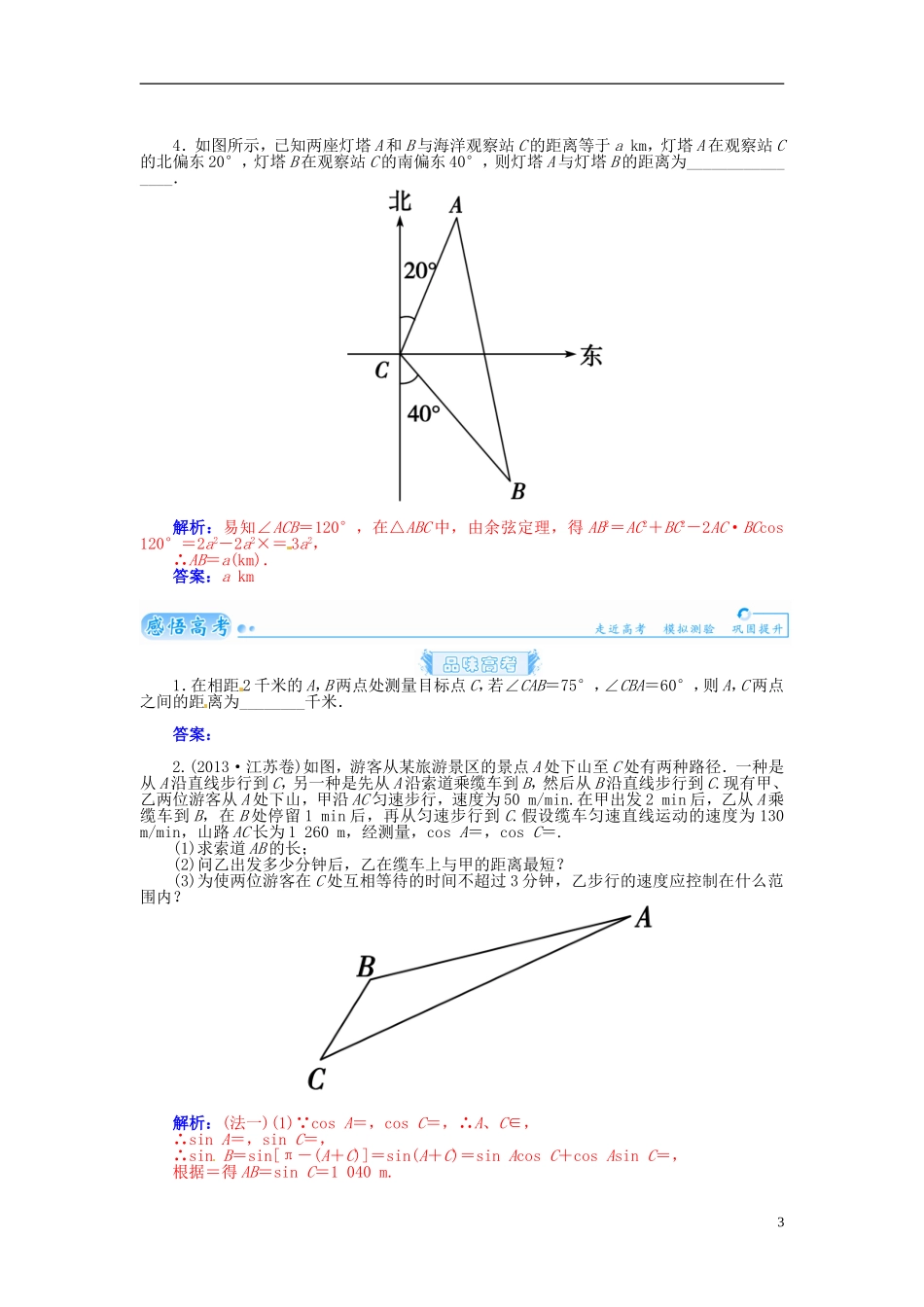
第八节 解三角形的应用知识梳理一、实际问题中的相关术语、名称1.方位角:指从正北方向顺时针转到目标方向线的夹角.2.方向角:相对于某正方向的水平角,如南偏东 30°,北偏西 45°,西偏北 60°等.3.仰角与俯角:指视线与水平线的夹角,视线在水平线上方的角叫仰角.视线在水平线下方的角叫俯角[如图(2)].4.坡度:坡面与水平面所成的二面角的度数[如图(3),角 θ 为坡角].坡比:坡面的铅直高度与水平长度之比如图(3),i=为坡比.(3)二、正、余弦定理可以解决的实际问题距离或宽度(有障碍物)、高度(底部或顶部不能到达)、角度(航海或航空定位)、面积等. 基础自测1.如下图,为了测量隧道口 AB 的长度,给定下列四组数据,测量时应当用数据( )1能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题. A.α,a,b B.a,b,γ C.α,β,a D.α,β,b解析:由于 A 与 B 不可到达,故不易测量 α,β,而 a,b,γ 容易测出.故选 B.答案:B2.如图所示,为测量一棵树的高度,在地面上选取 A,B 两点,从 A,B 两点分别测得树尖的仰角为 30°,45°,且 A,B 两点之间的距离为 60 m,则树的高度 h 为 ( ) A.(15+3)m B.(30+15)mC.(30+30)m D.(15+30)m解析:由正弦定理可得=,即 PB==,h=PBsin 45°==(30+30) m.故选 C.答案:C3.在地面上一点 D 测得一电视塔尖的仰角为 45°,再向塔底方向前进 100 m,又测得塔尖的仰角为 60°,则此电视塔高约为________.解析:如图,∠D=45°,∠A CB=60°,DC=100 m,∠DAC=15°,因为 AC=,所以 AB=AC·sin 60°===50(3+) m.答案:50(3+) m24.如图所示,已知两座灯塔 A 和 B 与海洋观察站 C 的距离等于 a km,灯塔 A 在观察站 C的北偏东 20°,灯塔 B 在观察站 C 的南偏东 40°,则灯塔 A 与灯塔 B 的距离为________________.解析:易知∠ACB=120°,在△ABC 中,由余弦定理,得 AB2=AC2+BC2-2AC·BCcos 120°=2a2-2a2×= 3a2,∴AB=a(km).答案:a km1.在相距 2 千米的 A,B 两点处测量目标点 C,若∠CAB=75°,∠CBA=60°,则 A,C 两点之间的距离为________千米.答案:2.(2013·江苏卷)如图,游客从某旅游景区的景点 A 处下山至 C 处有两种路径.一种是从 A 沿直线步行到 C,另一种是先从 A 沿索道乘缆车到 B,然后从 B...