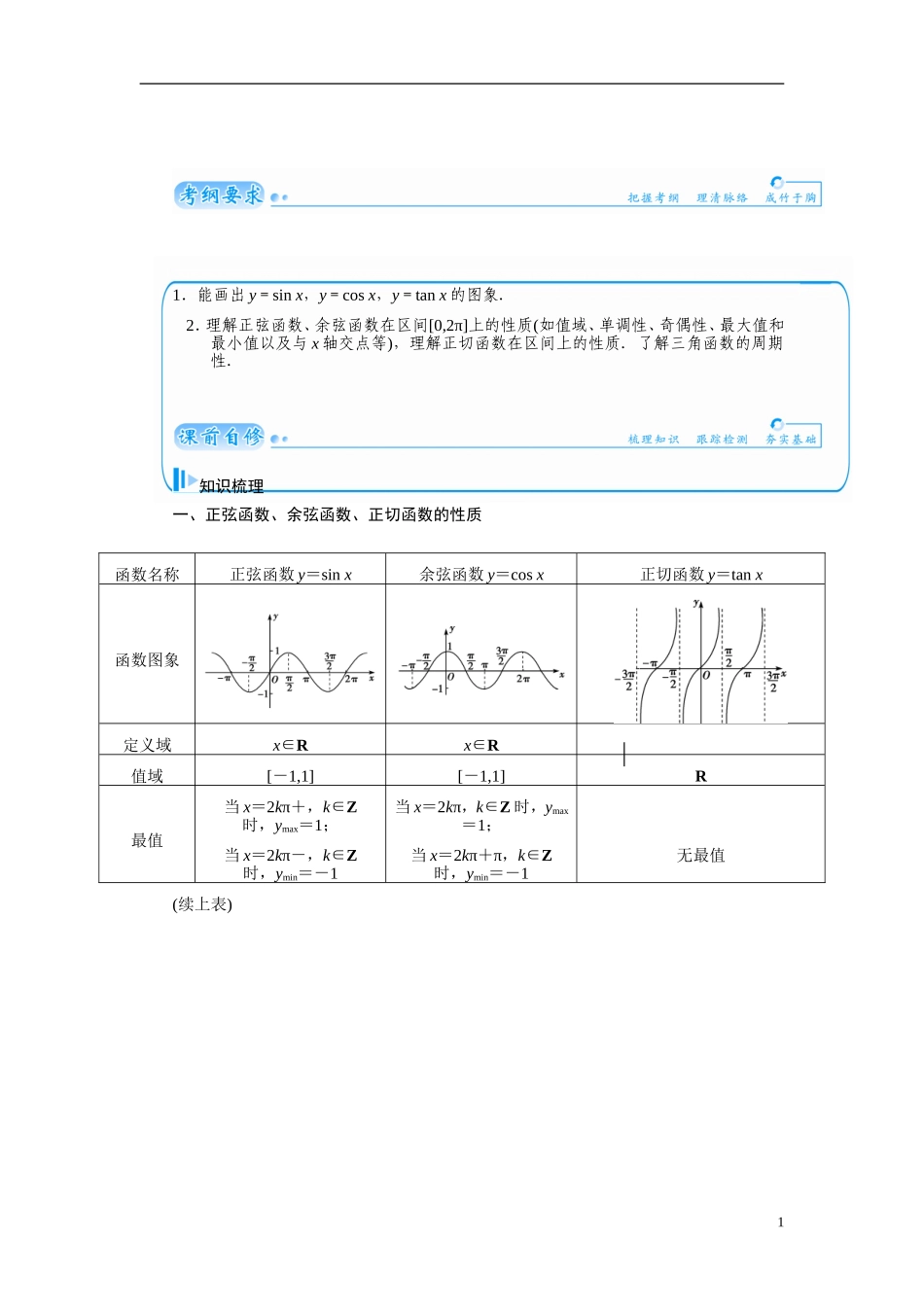
1.能画出 y=sin x,y=cos x,y=tan x 的图象.2.理解正弦函数、余弦函数在区间[0,2π]上的性质(如值域、单调性、奇偶性、最大值和最小值以及与 x 轴交点等),理解正切函数在区间上的性质.了解三角函数的周期性.知识梳理一、正弦函数、余弦函数、正切函数的性质函数名称正弦函数 y=sin x余弦函数 y=cos x正切函数 y=tan x函数图象定义域x∈Rx∈R值域[-1,1][-1,1]R最值当 x=2kπ+,k∈Z时,ymax=1;当 x=2kπ-,k∈Z时,ymin=-1当 x=2kπ,k∈Z 时,ymax=1;当 x=2kπ+π,k∈Z时,ymin=-1无最值(续上表)1二、研究函数 y=Asin(ωx+φ)性质的方法类比于研究 y=sin x 的性质,只需将 y=Asin(ωx+φ)中的 ωx+φ 看成 y=sin x 中的 x,但在求 y=Asin(ωx+φ)的单调区间时,要特别注意 A 和 ω 的符号,通过诱导公式先将 ω 化为正数.研究函数 y=Acos(ωx+φ),y=Atan(ωx+φ)的性质的方法与其类似,也是类比、转化.三、求三角函数的周期的常用方法经过恒等变形化成“y=Asin(ωx+φ),y=Acos(ωx+φ),y=Atan(ωx+φ)”的形式,再利用周期公式.如:函数 y=Asin(ωx+φ),y=Acos(ωx+φ)的最小正周期都是;函数 y=Atan(ωx+φ)的最小正周期是.另外还有图象法和定义法.基础自测1.(2013·揭阳二模)设函数 f(x)=cos(2π-x)+cos,则函数的最小正周期为( )A. B.π C.2π D.4π2解析:函数 f(x)=cos x+sin x=2=2sin,故其最小正周期为=2π,故选 C.答案:C2.(2013·天津卷)函数 f(x)=sin 在区间上的最小值为( )A.-1 B.- C. D.0解析:因为 x∈,所以-≤2x-≤,令 n=2x-,则 sin=sin n 在 n∈上的最小值为 sin=-.故选 B. 答案:B3.(2012·浙江名校新高考联盟二联) 若函数 f(x)=sin(x+α)-2cos(x-α)是奇函数,则 sin αcos α=________.解析:因为函数 f(x)=sin(x+α)-2cos(x-α)是奇函数,所以 f(0)=sin α-2cos α=0,即tan α=2.所以 sin αcos α>0,不妨设 α 为锐角,可得 sin α=,cos α=.所以 sin αcos α=.答案:4.(2012·合肥模拟)已知函数 f(x)=sin(ω>0)在上单调递增,在上单调递减,则 ω=___________.3 1.(2013·山东卷)函数 y=x co s x+sin x 的图象大致为( )解析:函数 y=xcos x+sin x 为奇函数,排除 B.取 x=,排除 C;...