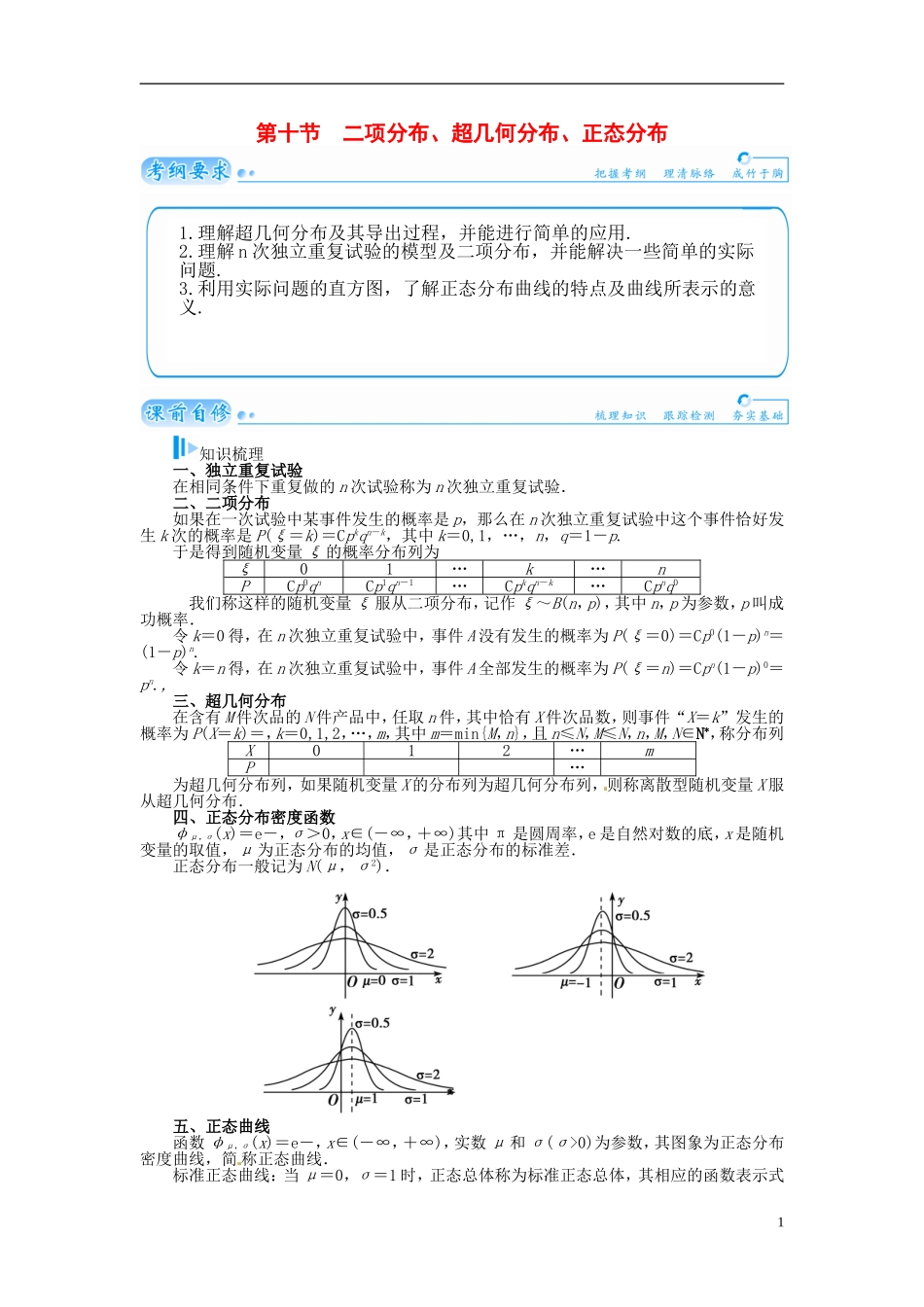
第十节 二项分布、超几何分布、正态分布知识梳理一、独立重复试验在相同条件下重复做的 n 次试验称为 n 次独立重复试验.二、二项分布如果在一次试验中某事件发生的概率是 p,那么在 n 次独立重复试验中这个事件恰好发生 k 次的概率是 P(ξ=k)=Cpkqn-k,其中 k=0,1,…,n,q=1-p.于是得到随机变量 ξ 的概率分布列为ξ01…k…nPCp0qnCp1qn-1…Cpkqn-k…Cpnq0 我们称这样的随机变量 ξ 服从二项分布,记作 ξ~B(n,p),其中 n,p 为参数,p 叫成功概率.令 k=0 得,在 n 次独立重复试验中,事件 A 没有发生的概率为 P(ξ=0)=Cp0(1-p)n=(1-p)n.令 k=n 得,在 n 次独立重复试验中,事件 A 全部发生的概率为 P(ξ=n)=Cpn(1-p)0=pn., 三、超几何分布在含有 M 件次品的 N 件产品中,任取 n 件,其中恰有 X 件次品数,则事件“X=k”发生的概率为 P(X=k)=,k=0,1,2,…,m,其中 m=min{M,n},且 n≤N,M≤N,n,M,N∈N*,称分布列X012…mP…为超几何分布列,如果随机变量 X 的分布列为超几何分布列,则称离散型随机变量 X 服从超几何分布.四、正态分布密度函数φμ,σ(x)=e-,σ>0,x∈(-∞,+∞)其中 π 是圆周率,e 是自然对数的底,x 是随机变量的取值,μ 为正态分布的均值,σ 是正态分布的标准差.正态分布一般记为 N(μ,σ2).五、正态曲线函数 φμ,σ(x)=e-,x∈(-∞,+∞),实数 μ 和 σ(σ>0)为参数,其图象为正态分布密度曲线,简 称正态曲线.标准正态曲线:当 μ=0,σ=1 时,正态总体称为标准正态总体,其相应的函数表示式11.理解超几何分布及其导出过程,并能进行简单的应用.2.理解 n 次独立重复试验的模型及二项分布,并能解决一些简单的实际问题.3.利用实际问题的直方图,了解正态分布曲线的特点及曲线所表示的意义.是 f(x)=e-,x∈(-∞,+∞)其相应的曲线称为标准正态曲线.六、正态分布如果对于任何实数 a