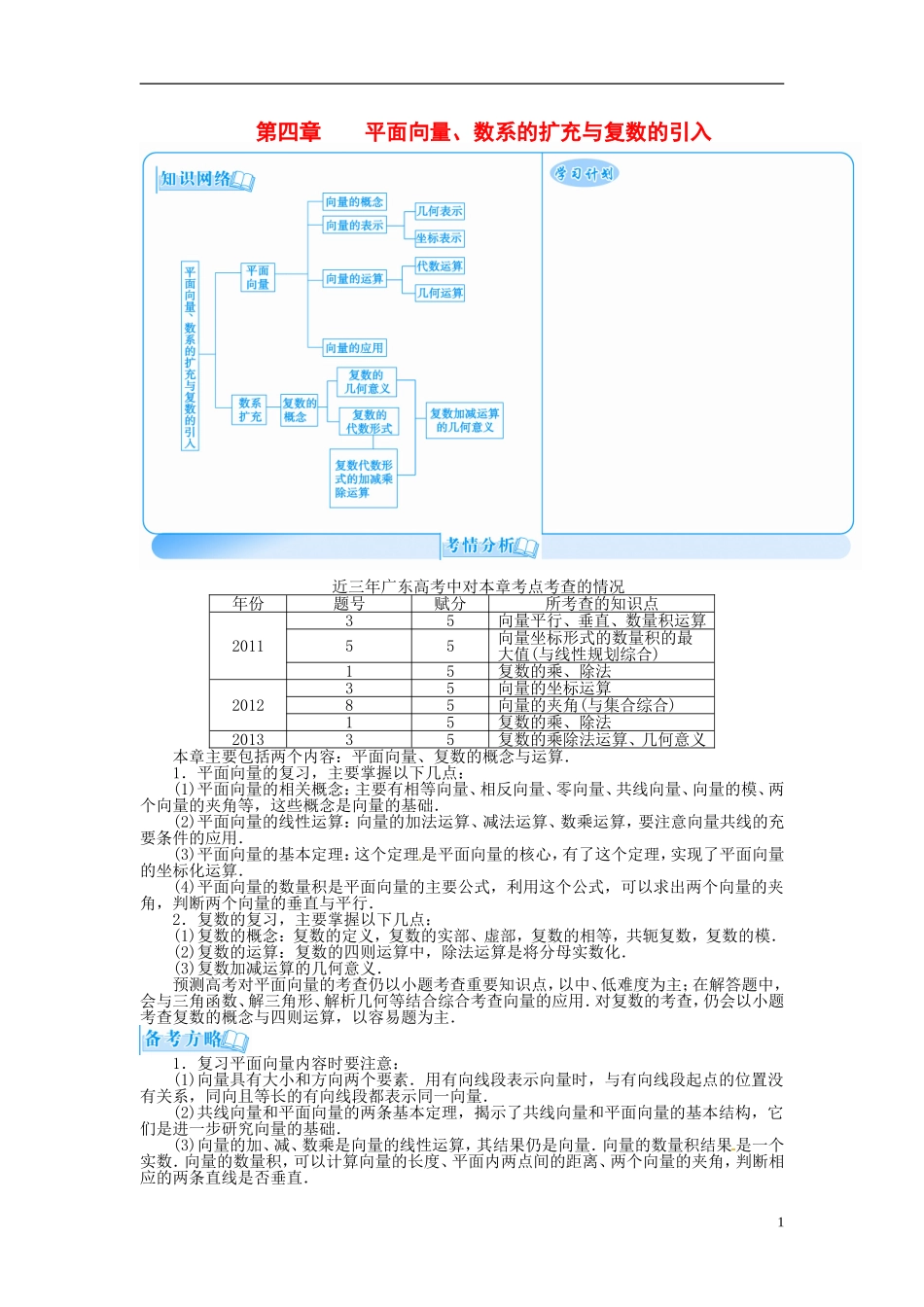
第四章 平面向量、数系的扩充与复数的引入近三年广东高考中对本章考点考查的情况年份题号赋分所考查的知识点201135向量平行、垂直、数量积运算55向量坐标形式的数量积的最大值(与线性规划综合)15复数的乘、除法201235向量的坐标运算85向量的夹角(与集合综合)15复数的乘、除法201335复数的乘除法运算、几何意义本章主要包括两个内容:平面向量、复数的概念与运算.1.平面向量的复习,主要掌握以下几点:(1)平面向量的相关概念:主要有相等向量、相反向量、零向量、共线向量、向量的模、两个向量的夹角等,这些概念是向量的基础.(2)平面向量的线性运算:向量的加法运算、减法运算、数乘运算,要注意向量共线的充要条件的应用.(3)平面向量的基本定理:这个定理是平面向量的核心,有了这个定理,实现了平面向量的坐标化运算.(4)平面向量的数量积是平面向量的主要公式,利用这个公式,可以求出两个向量的夹角,判断两个向量的垂直与平行.2.复数的复习,主要掌握以下几点:(1)复数的概念:复数的定义,复数的实部、虚部,复数的相等,共轭复数,复数的模.(2)复数的运算:复数的四则运算中,除法运算是将分母实数化.(3)复数加减运算的几何意义.预测高考对平面向量的考查仍以小题考查重要知识点,以中、低难度为主;在解答题中,会与三角函数、解三角形、解析几何等结合综合考查向量的应用.对复数的考查,仍会以小题考查复数的概念与四则运算,以容易题为主.1.复习平面向量内容时要注意:(1)向量具有大小和方向两个要素.用有向线段表示向量时,与有向线段起点的位置没有关系,同向且等长的有向线段都表示同一向量.(2)共线向量和平面向量的两条基本定理,揭示了共线向量和平面向量的基本结构,它们是进一步研究向量的基础.(3)向量的加、减、数乘是向量的线性运算,其结果仍是向量.向量的数量积结果 是一个实数.向量的数量积,可以计算向量的长度、平面内两点间的距离、两个向量的夹角,判断相应的两条直线是否垂直.1(4)向量的运算与实数的运算有异同点,学习时要注意这一点,如数量积不满足结合律.(5)要注意向量在几何、三角、物理学中的应用.(6)平面向量的数量积及坐标运算是高考的重点,复习中要注意培养准确的运算能力和灵活运用知识的.2.对于复数,《课标》及《考纲》的要求有以下三点:理解复数的基本概念,理解复数相等的充要条件,会进行复数代数形式的四则运算.所以在复习中应掌握好以下几个方面:(1)掌握好复数的基本概念...