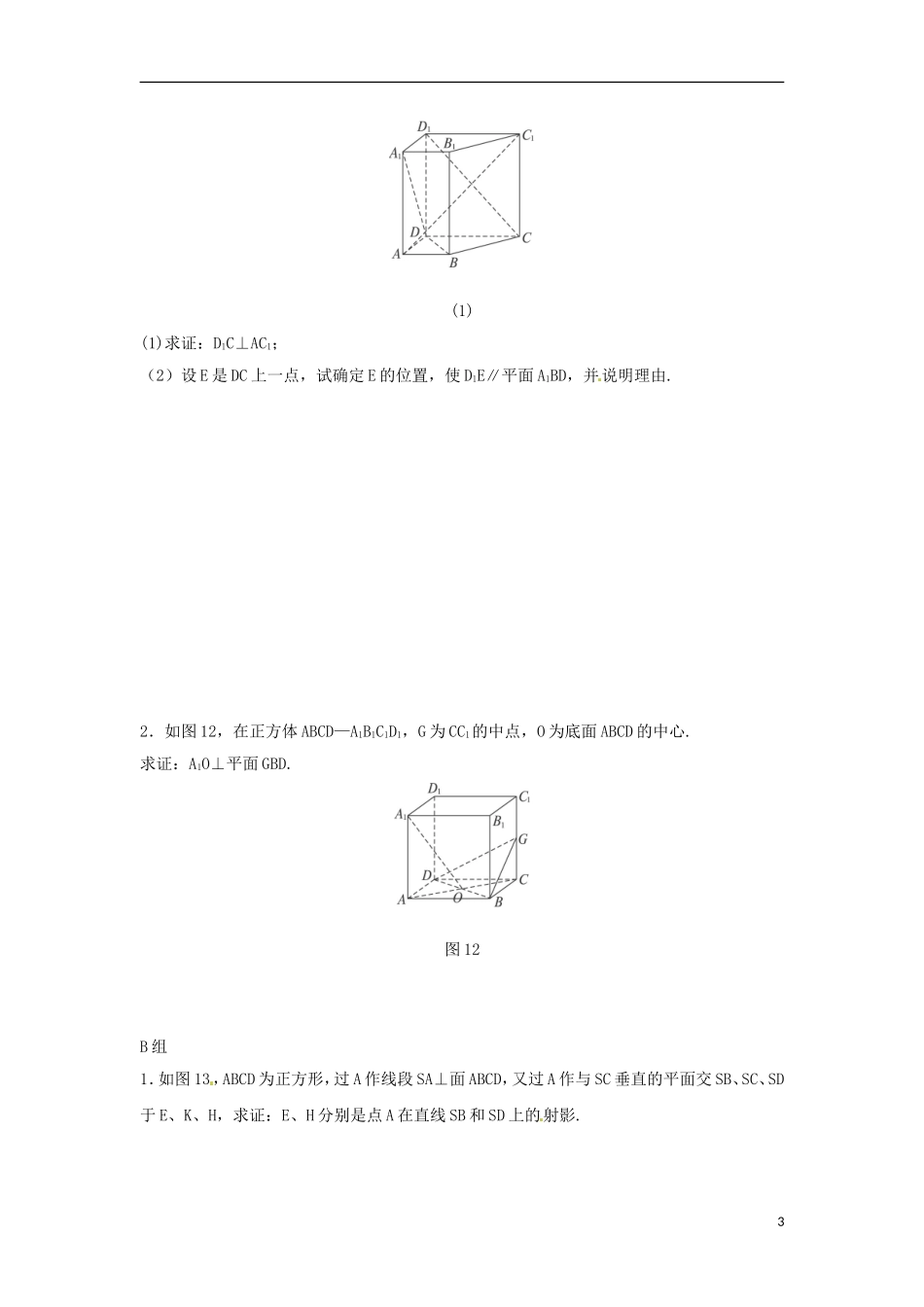
云南省德宏州潞西市芒市中学 2014 年高中数学 2.3.1 直线与平面垂直的判定学案 新人教 A 必修 2一、学习目标1.了解、感受直线和平面垂直的概念,体会探究判定直线和平面垂直的方法,掌握线面垂直的判定定理并能进行简单运用;2.加深对转化思想的认识,进一步熟练将空间问题化为平面问题加以解决的基本方法;3.正确理解直线和平面所成角的概念,掌握求线面角的基本方法;二、问题与例题1.创设情景,导入新课如果一条直线垂直于一个平面的无数条直线,那么这条直线是否与这个平面垂直?举例说明. 如图 1,直线 AC1与直线 BD、EF、GH 等无数条直线垂直,但直线AC1与平面 ABCD 不垂直.图 12.新知探究问题 1 怎样定义直线与平面垂直并画出图形?问题 2 探究直线与平面垂直的判定定理。问题 3 怎样用三种语言描述直线与平面垂直的判定定理?问题 4 探究斜线在平面内的射影,讨论直线与平面所成的角。问题 5 探究点到平面的距离。3.例题课本例 1、例 24.目标检测(1)证明:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于同一个平面。1 (2)如图 10,四面体 A—BCD 的棱长都相等,Q 是 AD 的中点,求 CQ 与平面 DBC 所成的角的正弦值.图 10三、配餐作业A 组1.如图 11(1),在直四棱柱 ABCD—A1B1C1D1中,已知 DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.2(1)(1)求证:D1C⊥AC1;(2)设 E 是 DC 上一点,试确定 E 的位置,使 D1E∥平面 A1BD,并说明理由.2.如图 12,在正方体 ABCD—A1B1C1D1,G 为 CC1的中点,O 为底面 ABCD 的中心.求证:A1O⊥平面 GBD.图 12B 组1.如图 13,ABCD 为正方形,过 A 作线段 SA⊥面 ABCD,又过 A 作与 SC 垂直的平面交 SB、SC、SD于 E、K、H,求证:E、H 分别是点 A 在直线 SB 和 SD 上的射影.3图 13C 组1.如图 15,已知 a、b 是两条相互垂直的异面直线,线段 AB 与两异面直线 a、b 垂直且相交,线段 AB 的长为定值 m,定长为 n(n>m)的线段 PQ 的两个端点分别在 a、b 上移动,M、N 分别是AB、PQ 的中点.图 15求证:(1)AB⊥MN;(2)MN 的长是定值.4