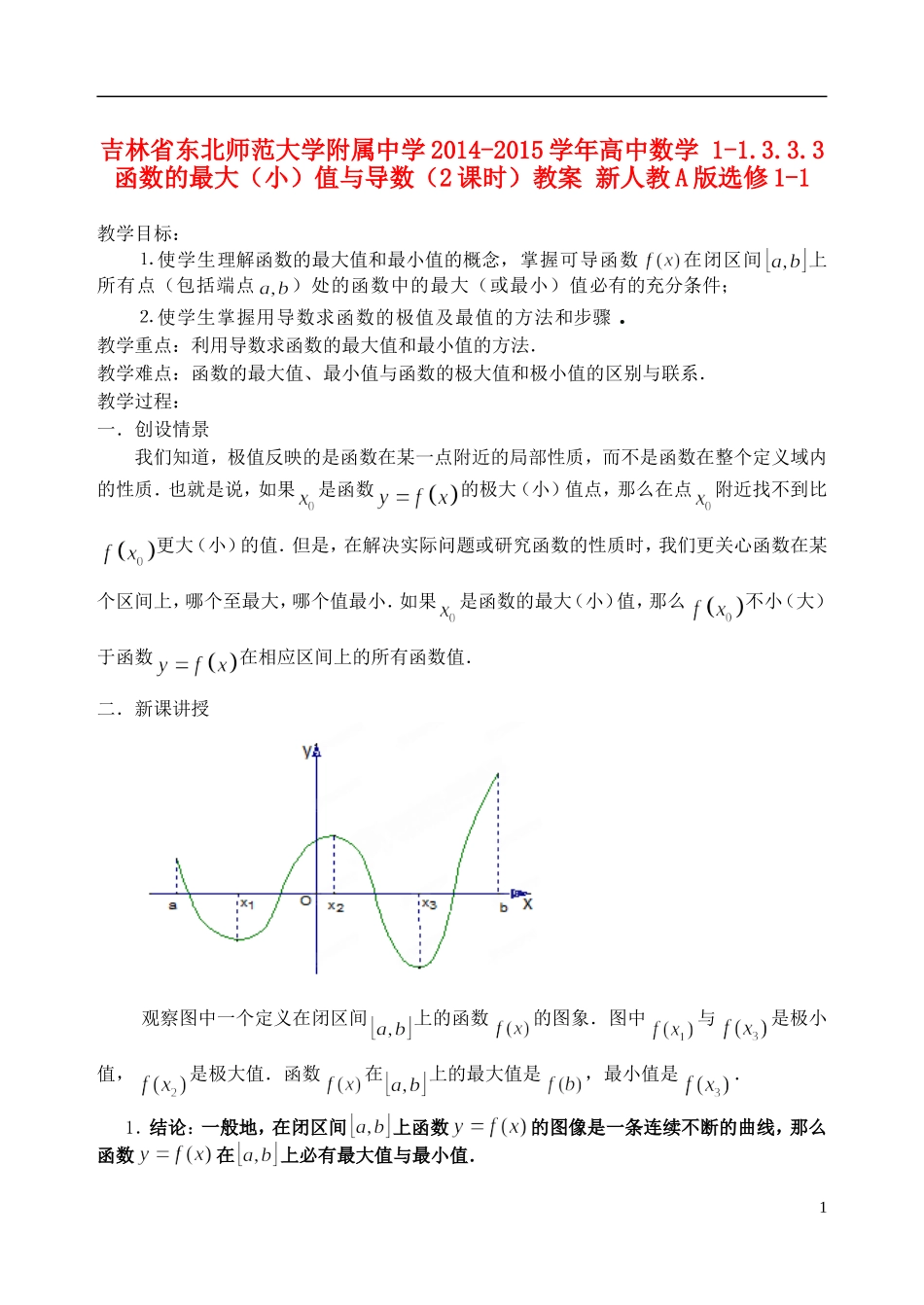
吉林省东北师范大学附属中学 2014-2015 学年高中数学 1-1.3.3.3函数的最大(小)值与导数(2 课时)教案 新人教 A 版选修 1-1教学目标:⒈ 使学生理解函数的最大值和最小值的概念,掌握可导函数在闭区间上所有点(包括端点)处的函数中的最大(或最小)值必有的充分条件;⒉ 使学生掌握用导数求函数的极值及最值的方法和步骤 奎屯王新敞新疆教学重点:利用导数求函数的最大值和最小值的方法.教学难点:函数的最大值、最小值与函数的极大值和极小值的区别与联系.教学过程:一.创设情景我们知道,极值反映的是函数在某一点附近的局部性质,而不是函数在整个定义域内的性质.也就是说,如果是函数的极大(小)值点,那么在点附近找不到比更大(小)的值.但是,在解决实际问题或研究函数的性质时,我们更关心函数在某个区间上,哪个至最大,哪个值最小.如果是函数的最大(小)值,那么不小(大)于函数在相应区间上的所有函数值.二.新课讲授观察图中一个定义在闭区间上的函数的图象.图中与是极小值,是极大值.函数在上的最大值是,最小值是.1.结论:一般地,在闭区间上函数的图像是一条连续不断的曲线,那么函数在上必有最大值与最小值.1说明:⑴如果在某一区间上函数的图像是一条连续不断的曲线,则称函数在这个区间上连续.(可以不给学生讲)⑵ 给定函数的区间必须是闭区间,在开区间内连续的函数不一定有最大值与最小值.如函数在内连续,但没有最大值与最小值;⑶ 在闭区间上的每一点必须连续,即函数图像没有间断,⑷ 函数在闭区间上连续,是在闭区间上有最大值与最小值的充分条件而非必要条件.(可以不给学生讲)2.“最值”与“极值”的区别和联系⑴ 最值”是整体概念,是比较整个定义域内的函数值得出的,具有绝对性;而“极值”是个局部概念,是比较极值点附近函数值得出的,具有相对性.⑵ 从个数上看,一个函数在其定义域上的最值是唯一的;而极值不唯一;⑶ 函数在其定义区间上的最大值、最小值最多各有一个,而函数的极值可能不止一个,也可能没有一个奎屯王新敞新疆⑷ 极值只能在定义域内部取得,而最值可以在区间的端点处取得,有极值的未必有最值,有最值的未必有极值;极值有可能成为最值,最值只要不在端点必定是极值.3.利用导数求函数的最值步骤:由上面函数的图象可以看出,只要把连续函数所有的极值与定义区间端点的函数值进行比较,就可以得出函数的最值了.一般地,求函数在上的最大值与最小...