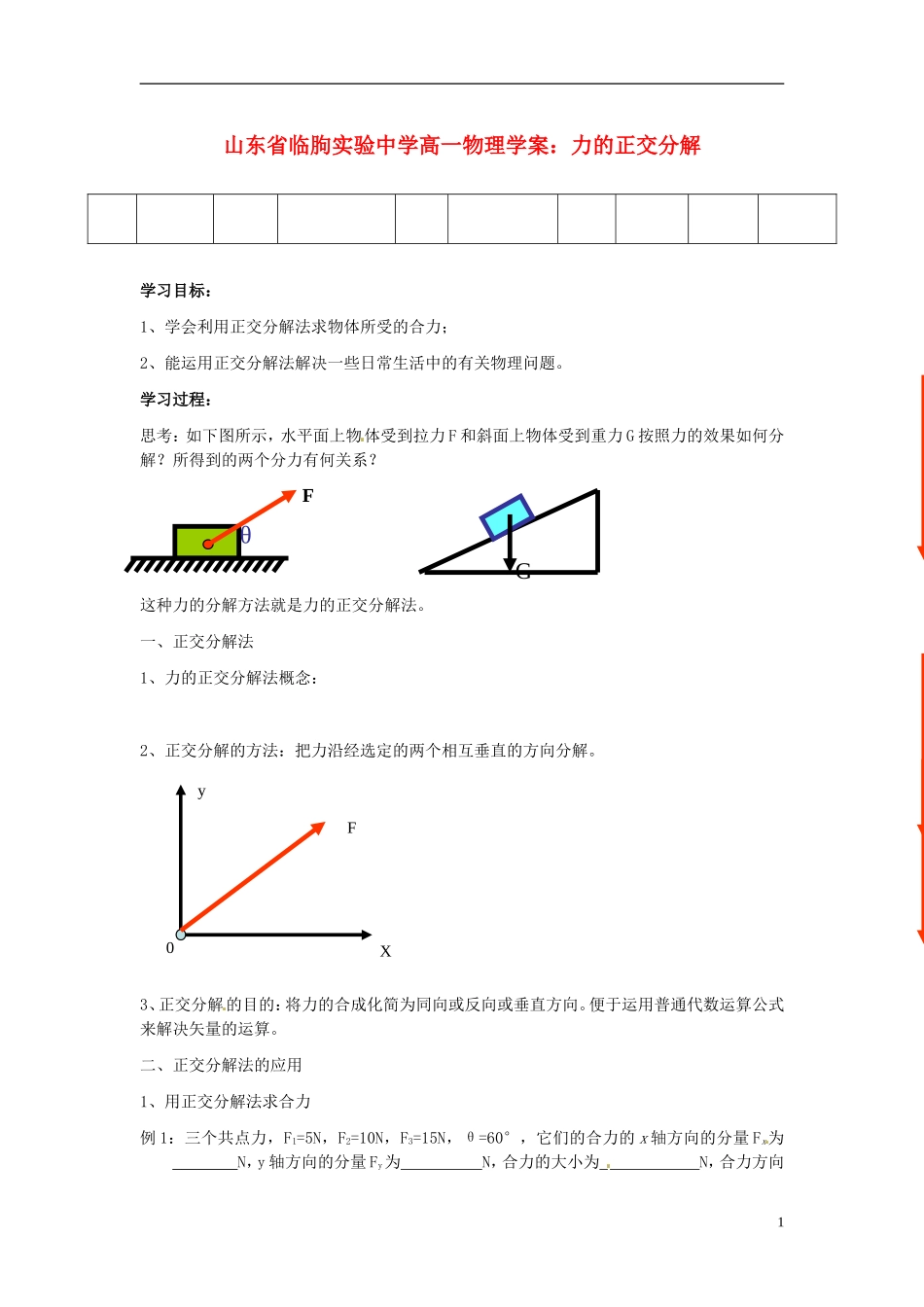
山东省临朐实验中学高一物理学案:力的正交分解学习目标:1、学会利用正交分解法求物体所受的合力;2、能运用正交分解法解决一些日常生活中的有关物理问题。学习过程:思考:如下图所示,水平面上物体受到拉力 F 和斜面上物体受到重力 G 按照力的效果如何分解?所得到的两个分力有何关系?这种力的分解方法就是力的正交分解法。一、正交分解法1、力的正交分解法概念:2、正交分解的方法:把力沿经选定的两个相互垂直的方向分解。3、正交分解的目的:将力的合成化简为同向或反向或垂直方向。便于运用普通代数运算公式来解决矢量的运算。二、正交分解法的应用1、用正交分解法求合力例 1:三个共点力,F1=5N,F2=10N,F3=15N,θ=60°,它们的合力的 x 轴方向的分量 Fx为 ________N,y 轴方向的分量 Fy为 N,合力的大小为 N,合力方向1FθG0XyF与 x 轴正方向夹角为 。问题 1、力的正交分解适用什么情况?问题 2:坐标轴如何选取?问题 3:利用正交分解法求合力的一般步骤?练习 1、同在 xOy 平面内的六个力如图所示,大小分别为 F1=10N,F2=20N,F3=12N,F4=10N,F5=30N, F6=12N,求合力的大小和方向。2 正交分解在平衡问题中的应用例 2、如图所示,用绳 AO 和 BO 吊起一个重 100N 的物体,两绳 AO、BO 与竖直方向的夹角分别为 30o和 45o,求绳 AO 和 BO 对物体的拉力的大小。2xF5F3F2F1y30°30°30°F6F4问题 4、总结利用正交分解法解决平衡问题的一般步骤。练习 2、如图所示,θ=370,sin370=0.6,cos370=0.8。箱子重 G=200N,箱子与地面的动摩擦因数 μ=0.30。要匀速拉动箱子,拉力 F 为多大? 随堂检测:1、三个共点力 F1=20N、F2=30N、F3=40N,它们相互间的夹角为 120o,求它们的合力大小。2、如图所示,在倾角为 α=37°的斜面上有一块竖直放置的档板,在档板和斜面之间放一个重力 G=20N 的光滑球处于静止状态,求小球受到的挡板的支持力 F1 和受到斜面的支持力 F2的大小。(sin370=0.6,cos370=0.8)3ABO30o45o3、如图,位于水平地面上的质量为M 的小木块,在大小为 F、方向与水平方向成 a 角的拉力作用下沿地面作匀速直线运动。求:(1)地面对物体的支持力?(2)木块与地面之间的动摩擦因数?4、长为 20cm 的轻绳 BC 两端固定在天花板上,在中点系上一重 60N 的重物,如图所示:(1)当 BC 的距离为 10cm 时,AB 段绳上的拉力为多少?(2)当 BC 的距离为 10cm 时.AB 段绳上的拉力为多少? 4